Projectile launched from an inclined plane strikes a wall horizontally

[subhradeep mahata]

Homework Statement

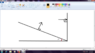
There is an inclined plane which is inclined at an angle of 37° to the horizontal. A projectile is projected perpendicularly to the inclined plane at a velocity of 50m/s such that it strikes a wall kept at the foot of the inclined plane perpendicularly. Find the time taken to reach the wall.

Homework Equations

The Attempt at a Solution

I have correctly done this problem when we consider the x and y-axis vertically (wrt ground). The trick in this problem is that it has reached the maximum height just when it strikes the wall.
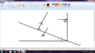
But, I am not getting the correct answer when I consider the x and y-axis along the inclined plane. My "faulty" method is described below:

As it reaches max height, y component of velocity decreases from 50 to 0. So, applying v=u+at in y-direction,
0=50+(-gcos37°)(t)
or, t=6.25 sec , which is 2.25 seconds more than what i got as the correct answer in my first method.
Please see where i went wrong.

 

[TSny]

As it reaches max height, y component of velocity decreases from 50 to 0.

When the y-axis is perpendicular to the incline, is it correct to take the y-component of velocity to be zero at maximum height above the floor?

 

[subhradeep mahata]

I can't find anything wrong. Please explain.

 

[TSny]

The projectile is moving perpendicular to the wall when it hits the wall. If a vector is perpendicular to the wall, it can't also be perpendicular to your y-axis. Therefore, the vector cannot have a zero y-component.

 

[subhradeep mahata]

All right, got it.
So, basically it is sensible to take the y-axis parallel to the wall like in my first method, isn't it?
Is there any way to proceed from here?

 

[TSny]

All right, got it.
So, basically it is sensible to take the y-axis parallel to the wall like in my first method, isn't it?

Yes. I think it is easiest to have the y-axis parallel to the wall.

Is there any way to proceed from here?

You can work the problem with the y-axis chosen perpendicular to the incline. You will need to think about the relation between the x and y components of the velocity at the moment the projectile hits the wall.

 

[subhradeep mahata]

Okay, I will try it.
@TSny Thank you very much.

 

[TSny]

You are welcome. Have fun with it.