- #1
fizixfan
- 105
- 33
I developed two algorithms for calculating the density of close packed congruent identical spheres in two different arrangements:
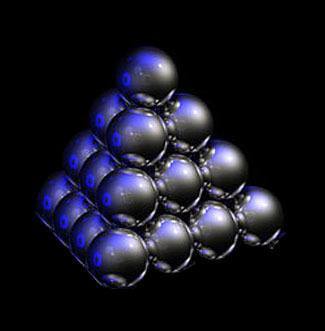
Figure 1. Tetrahedral ball stack.

Figure 2. Square pyramidal ball stack.
Here are the Excel-friendly algorithms (n = number of spheres along bottom row):
Density of Tetrahedral Stack (Dt):
Dt = (4*(2^0.5)*n*(n+1)*(n+2)*Pi())/(3*(2*n+2*3^0.5-2)^3 or
 (1)
(1)
Density of Square Pyramidal Stack (Dp):
Dp = ( n*(1+n)*(1+2*n)*Pi())/(3*((1+(2^0.5*n)))^3) or
 (2)
(2)
I found that, as the number of spheres approaches infinity for both arrangements, that Dt = Dp = ≈ 0.74048... or π/√18.
I resorted to Wolfram Alpha with the following query:
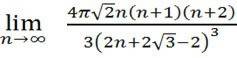 =
=
 (3)
(3)
and got the following result:
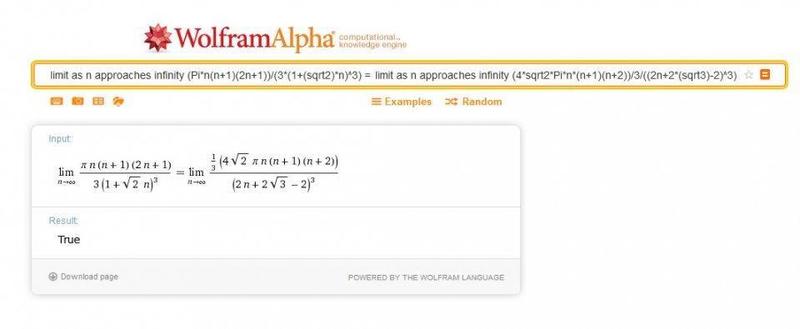 (4)
(4)
True!
I then forwarded my calculations to Dr. Thomas C. Hales, who proved the Kepler Conjecture, asking him if Dt = Dp was correct, and he responded, saying,
"The reason for the equal densities in a tetrahedron and square pyramid is that they can both be viewed as part of the face-centered-cubic packing, each with a different set of exposed facets."
My question to you is this: can you provide a detailed proof that (1) = (2) as n→∞, i.e., that
 is true?
is true?
Thanks for any input!
Fizixfan.
- A tetrahedron with four equilateral triangular faces, and
- A square pyramid with a square base and four equilateral triangular faces, as shown below.
Figure 1. Tetrahedral ball stack.
Figure 2. Square pyramidal ball stack.
Here are the Excel-friendly algorithms (n = number of spheres along bottom row):
Density of Tetrahedral Stack (Dt):
Dt = (4*(2^0.5)*n*(n+1)*(n+2)*Pi())/(3*(2*n+2*3^0.5-2)^3 or
Density of Square Pyramidal Stack (Dp):
Dp = ( n*(1+n)*(1+2*n)*Pi())/(3*((1+(2^0.5*n)))^3) or
I found that, as the number of spheres approaches infinity for both arrangements, that Dt = Dp = ≈ 0.74048... or π/√18.
I resorted to Wolfram Alpha with the following query:
and got the following result:
True!
I then forwarded my calculations to Dr. Thomas C. Hales, who proved the Kepler Conjecture, asking him if Dt = Dp was correct, and he responded, saying,
"The reason for the equal densities in a tetrahedron and square pyramid is that they can both be viewed as part of the face-centered-cubic packing, each with a different set of exposed facets."
My question to you is this: can you provide a detailed proof that (1) = (2) as n→∞, i.e., that
Thanks for any input!
Fizixfan.