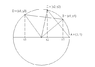
SUMMARY
The forum discussion centers on the proofs for the trigonometric addition formulas: sin(A+B), sin(A-B), cos(A+B), and cos(A-B). Users provide geometric and algebraic approaches to derive these identities, emphasizing the use of the unit circle and the co-function identities. The discussion highlights that sin(A-B) and cos(A-B) can be derived from sin(A+B) and cos(A+B) respectively, utilizing the properties of sine and cosine for negative angles. Additionally, a diagrammatic proof is suggested to enhance understanding.
PREREQUISITES
- Understanding of trigonometric functions and identities
- Familiarity with the unit circle and its properties
- Basic knowledge of geometric proofs
- Experience with complex numbers and Euler's formula
NEXT STEPS
- Study the derivation of trigonometric identities using the unit circle
- Learn about the co-function identities in trigonometry
- Explore geometric proofs for trigonometric functions
- Investigate Euler's formula and its applications in trigonometry
USEFUL FOR
Mathematicians, physics students, educators, and anyone interested in deepening their understanding of trigonometric identities and their proofs.