The_Logos
- 8
- 0
Does anybody knows how you can reach one form of the divergence formula from the other? Or in general, why is the equivalence
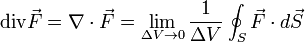 true?
true?
The equivalence between the nabla form and the integral form of divergence is established through Gauss' divergence theorem. In a 3D Euclidean space, the theorem demonstrates that the total flux across a boundary surface is equal to the volume integral of the divergence within that volume. As the radius of the solid ball approaches zero, the approximation improves, leading to a formal proof of the equivalence. This discussion emphasizes the historical context of differential equations in relation to their integral counterparts.
PREREQUISITESMathematicians, physics students, and anyone interested in vector calculus and the foundational principles of divergence in mathematical analysis.
The formula is a direct consequence of Gauss' divergence theorem. You may look at the things in the following manner.The_Logos said:Does anybody knows how you can reach one form of the divergence formula from the other? Or in general, why is the equivalencetrue?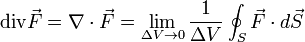
mathman said:
zoki85 said:The formula is a direct consequence of Gauss' divergence theorem. You may look at the things in the following manner.
Suppose p is a point in 3D Euclidean space. Let Er be a solid ball centered at p with radius r , and let Sr be the boundary surface of Er with outward pointing normal (and F is the vector field). Using Gauss' theorem we have:
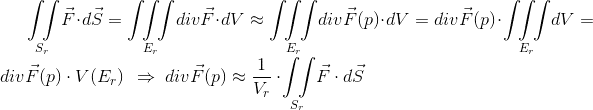
This aproximation improves as radius gets smaller, and in the limit (for r → 0 ⇒ Vr → 0) the equality holds.
Hope this helps.
Meh, my "logos" is quite irrational in everyday life, so I don't think that user name would suit me fine. And, althought short, this is kind of a sloppy proof. It's more a demonstration by Gauss' D.T. why it holds true. I guess a pro-mathematcian should feel a need to "polish" it, to write more rigouros proof. I agree there must be other ways to prove the formula (without G.D.T.) but I didn't try it.The_Logos said:That is just beautiful! you should just go ahead and take my user name, you are definitely more the logos than me! I wasted all day trying to make linear transformations thinking that it was my only hope (And managed nothing).
I actually was seeking for the proof of the equivalence before giving deep thought to the divergence theorem, just to find out that ironically I needed it to prove what apparently came before!.