Rinzler09
- 3
- 0
There is this T.a rule in laws of motion which can be applied to a system to solve problems regarding constraint motion. Here's an example
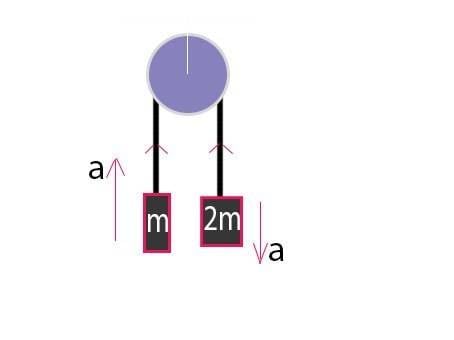
This example is pretty simple so I've decided to show the application of the rule here.
Consider the FBD of m,
T is in the same direction as the acceleration. Therefore, T.a=Ta1
Considering the FBD of 2m,
T is in the opposite direction. Therefore, T.a=-Ta2
ΣT.a=0, Therefore, Ta1 - Ta2=0
Thus, a1=a2
This method is really useful for complex pulley systems such as this one.
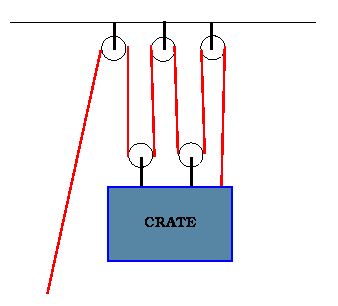
I was wondering how to prove this. Can somebody help? Just give me an idea. Don't post the proof.
This example is pretty simple so I've decided to show the application of the rule here.
Consider the FBD of m,
T is in the same direction as the acceleration. Therefore, T.a=Ta1
Considering the FBD of 2m,
T is in the opposite direction. Therefore, T.a=-Ta2
ΣT.a=0, Therefore, Ta1 - Ta2=0
Thus, a1=a2
This method is really useful for complex pulley systems such as this one.
I was wondering how to prove this. Can somebody help? Just give me an idea. Don't post the proof.