Whitehole
- 128
- 4
I'm reading the book by Zee, I came across a paragraph saying that the world is not flat.
"Given an airline table of distances, you can deduce that the world is curved without ever going outside. If I tell you the three distances between Paris, Berlin, and Barcelona, you can draw a triangle on a flat piece of paper with the three cities at the vertices. But now if I also give you the distances between Rome and each of these three cities, you would find that you can’t extend the triangle to a planar quadrangle (figure 1). So the distances between four points suffice to prove that the world is not flat."
What does he mean by "You would find that you can’t extend the triangle to a planar quadrangle. So the distances between four points suffice to prove that the world is not flat."? I can't depict what he wants to say here, can anyone help explain this?
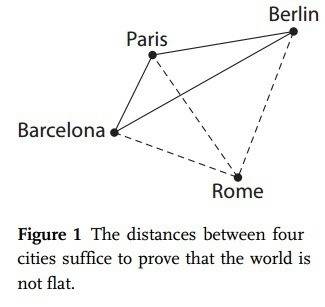
"Given an airline table of distances, you can deduce that the world is curved without ever going outside. If I tell you the three distances between Paris, Berlin, and Barcelona, you can draw a triangle on a flat piece of paper with the three cities at the vertices. But now if I also give you the distances between Rome and each of these three cities, you would find that you can’t extend the triangle to a planar quadrangle (figure 1). So the distances between four points suffice to prove that the world is not flat."
What does he mean by "You would find that you can’t extend the triangle to a planar quadrangle. So the distances between four points suffice to prove that the world is not flat."? I can't depict what he wants to say here, can anyone help explain this?