woundedtiger4
- 188
- 0
I know that f(A∩B) is not equal to f(A) ∩ f(B) but i don't know that where am i wrong in the following proof...:( can someone please give me an intuitive example?
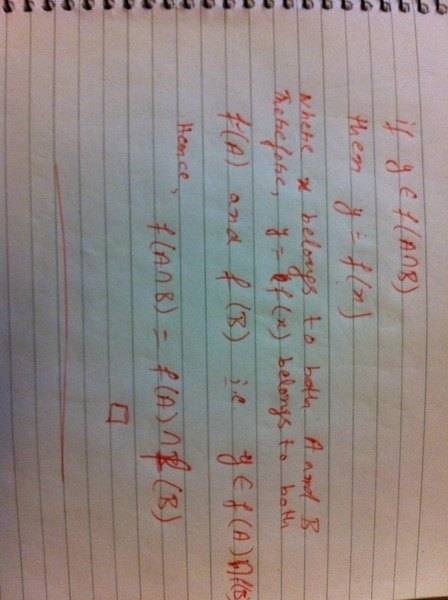
Thank you sir.HallsofIvy said:In order to prove "X= Y" you must prove both "X\subseteq Y" and Y\subseteq X.
You want to prove that f(A\cap B) is not equal to f(A)\cap f(B) and your give proof shows only that f(A\cap B)\subseteq f(A)\cap f(B).
So look for a counter example in which f(A)\cap f(B) is NOT a subset of f(A\cap B).
That is, find a function f and values p and q, p in A, q in B such that f(p)= f(q).