Qemikal
- 14
- 2
Hi, guys, i made an exercise, can you prove this?
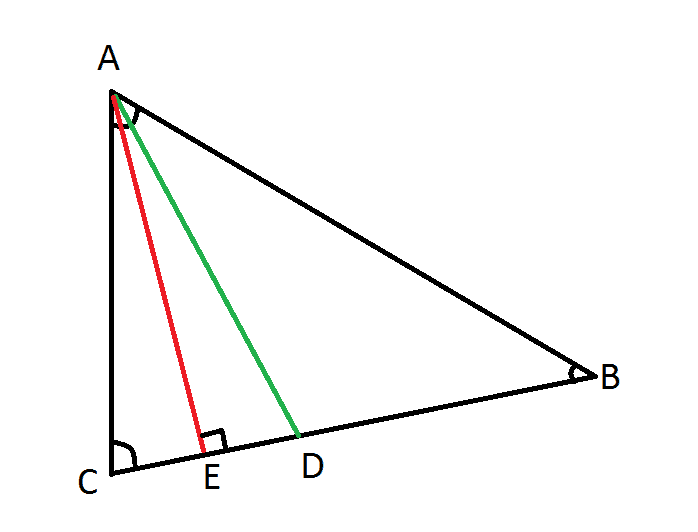
m(∠EAD)=[m(∠ABC)-m(∠ACB)]/2
If you have 5 free minutes, try it, i hope you'll like it!
It's my first own exercise, so I would like some feedback, too.
AD= bisecting(splits angle in 2 equal sides)
m(∠EAD)=[m(∠ABC)-m(∠ACB)]/2
If you have 5 free minutes, try it, i hope you'll like it!
It's my first own exercise, so I would like some feedback, too.
AD= bisecting(splits angle in 2 equal sides)
Last edited: