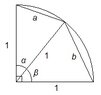
SUMMARY
The discussion focuses on proving the quadratic inequality of points on a semicircle O, specifically demonstrating that for points A, B, C, D on the semicircle with given lengths AB=a, BC=b, CD=c, DE=d, and AE=2, the inequality $a^2+b^2+c^2+d^2+abc+bcd < 4$ holds true. The proof utilizes the Law of Cosines and a function derived from the angles $\alpha$ and $\beta$, leading to the conclusion that $f(\alpha)<1$ for $0<\alpha<\frac{\pi}{2}$. The critical value of $\alpha$ is approximately 1.0605, confirming the inequality through endpoint evaluations.
PREREQUISITES
- Understanding of the Law of Cosines
- Familiarity with quadratic inequalities
- Knowledge of semicircles and their properties
- Basic calculus, specifically differentiation and critical points
NEXT STEPS
- Study the Law of Cosines in detail
- Explore advanced topics in quadratic inequalities
- Learn about the properties of semicircles and their geometric implications
- Investigate numerical root-finding techniques for critical values
USEFUL FOR
Mathematicians, geometry enthusiasts, and students studying inequalities and trigonometric properties in geometry will benefit from this discussion.