Prove that dim(V⊗W)=(dim V)(dim W)

[Karl Karlsson]

TL;DR

This proof was in my book.
(see image below)
Tensor product definition according to my book: $$V⊗W=\{f: V^*\times W^*\rightarrow k | \textrm {f is bilinear}\}$$ wher $V^*$ and $W^*$ are the dual spaces for V and W respectively.

I don't understand the step where they say $(e_i⊗f_j)(φ,ψ) = φ(e_i)ψ(f_j)$. Why is this equality true? What definition has been used? My understanding for all of this is still quite basic.

This proof was in my book.

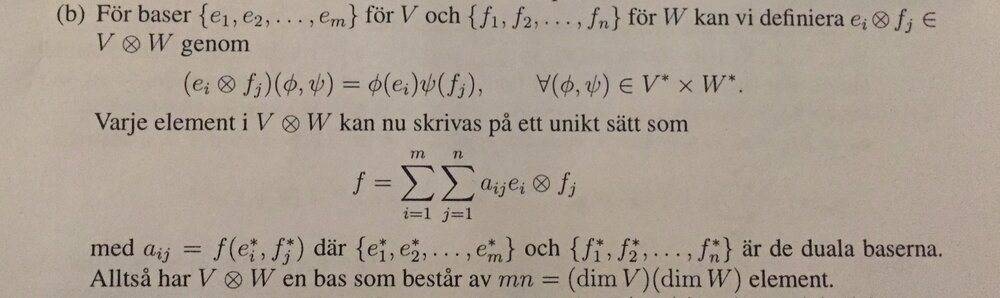
Tensor product definition according to my book: $$V⊗W=\{f: V^*\times W^*\rightarrow k | \textrm {f is bilinear}\}$$ wher $V^*$ and $W^*$ are the dual spaces for V and W respectively.

I don't understand the step where they say $(e_i⊗f_j)(φ,ψ) = φ(e_i)ψ(f_j)$. Why is this equality true? What definition has been used? My understanding for all of this is still quite basic.

Thanks in advance!

 

[member 587159]

This is true because they define it that way. By definition, $e_i \otimes f_j$ is the bilinear map defined by $$e_i \otimes f_j: V^* \times W^* \to k: (\phi, \psi) \mapsto \psi(e_i) \psi(f_j)$$
It is just a definition. The only thing you should check is that this map is indeed $k$-bilinear. We then obtain that $e_i \otimes f_j \in V \otimes W$ and it is then checked that $\{e_i \otimes f_j\}_{(i,j)}$ is a basis for $V \otimes W$ and since this basis has $\dim V \dim W$ amount of elements, you can conclude $\dim(V \otimes W) = \dim V \dim W$.

 

[fresh_42]

It should have been part of the definition. As it is written, it suggests that it cannot be done otherwise, which would require a proof. However, uniqueness of the tensor product is easier to prove in the language of categories, rather than using coordinates. The way it was done in the book is a mixture of both - neither done rigorously. The shortest way out of the dilemma is to incorporate it in the definition:
$$
T\in V\otimes W \Longleftrightarrow T=\sum_{\rho=1}^R v_{\rho} \otimes w_{\rho} \, : \,(X,Y)\longmapsto \sum_{\rho=1}^R v_{\rho}(X) \cdot w_{\rho}(Y) \in k
$$
for some $v_{\rho}\in V^*,w_{\rho}\in W^*$ and all $X\in V, Y\in W.$