Prove that triangle BAD is isosceles and....

[mathlearn]

Problem

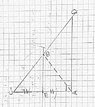
In the $\triangle ADC$ , $\angle DAC$ or angle $A$ is a right angle, E is the midpoint of AC . The perpendicular drawn to $AC$ from $E$ meets $DC$ at $B$

i.Drawn the given information in a figure & prove that $\triangle BAD$ is isosceles

ii. $AC^2+AD^2=4AB^2$

Diagram


View attachment 6047

Where do I need help

In proving that $\triangle BAD$ is isosceles & $AC^2+AD^2=4AB^2$

This is the first time I attempt to do this kind of a problem (Clapping)

Many Thanks :)

 

[Greg]

i) Start from the fact that B is the midpoint of CD (midpoint theorem).

ii) Start with the fact that 2AB = CD.

 

[mathlearn]

i) Start from the fact that B is the midpoint of CD (midpoint theorem).

ii) Start with the fact that 2AB = CD.

Thank you very much (Happy)

ii) Start with the fact that 2AB = CD

May i know the theorem or the case please :)

So $CB=BD$ (Converse of midpoint theorem)

& as $2AB = CD$ | $\therefore AB= \frac{1}{2} CD$ | $\frac{1}{2} CD $= CB or BD

$BA= BD$ | $\therefore \triangle BAD $ is isosceles

Correct?

In the first instance is it the Converse of the Midpoint theorem

The straight line through the midpoint of one side of a triangle and parallel to another side, bisects the third side.

or

the Midpoint theorem

The straight line segment through the midpoints of two sides of a triangle is
parallel to the third side and equal in length to half of it

 

[Greg]

Let's start with i) because we may use the results of i) to prove ii).

I'd like you to consider the problem carefully and decide which aspect of the midpoint theorem applies to which part of i). Post back with your answer and include your reasoning.

One way to solve i): consider a rectangle with diagonal BD and a rectangle with diagonal AB. Can you, using the midpoint theorem, show that these two rectangles are congruent? What famous theorem tells us that AB = BD?

 

[mathlearn]

Let's start with i) because we may use the results of i) to prove ii).

I'd like you to consider the problem carefully and decide which aspect of the midpoint theorem applies to which part of i). Post back with your answer and include your reasoning.

One way to solve i): consider a rectangle with diagonal BD and a rectangle with diagonal AB. Can you, using the midpoint theorem, show that these two rectangles are congruent? What famous theorem tells us that AB = BD?

Hey greg1313 :)

The triangle $CBE$ is equal to $ABE$ because they have equal angle in $E$ and equal sides $CE=EA$ and $BE=BE$.

So now what I have is $CB=BA$

Then the theorem should be the converse of the midpoint theorem

The straight line through the midpoint of one side of a triangle and parallel to another side, bisects the third side.

Many Thanks :)