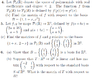Proving a Basis for a Vector Space

[shaon0]

Homework Statement

See Attachment.

The Attempt at a Solution

For the first two questions, I know I have to sub in values for a and b. But, I'm not sure what the output matrix is.
The 3rd q, to prove B is Basis for R^3. I just have to row reduce [(1,5);(1,6)] to get [(1,0);(0,1)] right? But like before, I don't know how to do b).

Any help is appreciated.

 

[HallsofIvy]

To find the matrix representing a given linear transformation, in a given ordered basis, apply the linear transformation to each basis vector in turn. Write the result as a linear combination of the basis vectors. The coefficients give the columns of the matrix.

For example, f(x^2)= (x^2)'= 2x= 2(1+ x)- 2(1)= -2(1)+ 2(1+ x)+ 0(x^2). Since the basis is \{1, 1+ x, x^2\}, in that order, the third column of the matrix would be
\begin{bmatrix}-2 \\ 2 \\ 0\end{bmatrix}


For 6(b) there are two different ways to do this. The most direct would be to use the matrix, as given, to determine T\left(\begin{array}{c} 1 \\ 5\end{array}\right) and T\left(\begin{array}{c}1 \\ 6\end{array}\right) and then write the results as linear combinations of those new basis vectors. Another would be to construct the "change of basis" matrix and multiply by that.

 

[shaon0]

To find the matrix representing a given linear transformation, in a given ordered basis, apply the linear transformation to each basis vector in turn. Write the result as a linear combination of the basis vectors. The coefficients give the columns of the matrix.

For example, f(x^2)= (x^2)'= 2x= 2(1+ x)- 2(1)= -2(1)+ 2(1+ x)+ 0(x^2). Since the basis is \{1, 1+ x, x^2\}, in that order, the third column of the matrix would be
\begin{bmatrix}-2 \\ 2 \\ 0\end{bmatrix} For 6(b) there are two different ways to do this. The most direct would be to use the matrix, as given, to determine T\left(\begin{array}{c} 1 \\ 5\end{array}\right) and T\left(\begin{array}{c}1 \\ 6\end{array}\right) and then write the results as linear combinations of those new basis vectors. Another would be to construct the "change of basis" matrix and multiply by that.

Thanks HallsOfIvy; I still don't understand how to do the other two though. My approach is sub in values for a and b which correspond to the co-effs. of the given basis. Then assemble a matrix from them. Eg: f[(5,0);(1,3)]=[(1,1);(2;-1)] which gives me [(-17,4);(15,-3)] for c).