ainster31
- 158
- 1
Why is the math in the red box necessary? According to this definition, it isn't:
ainster31 said:Why is the math in the red box necessary? According to this definition, it isn't:
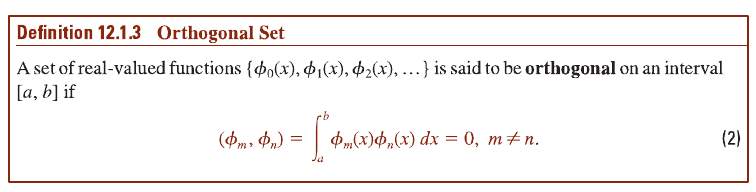
 …
…tiny-tim said:hi ainster31!
sorry, i don't understand your question…
the red box proves that (φ0, φn) = 0 (for n ≠ 0)
dextercioby said:m=0 is contained as a particular case for arbitrary m and n. It's no need to make the particular case.
dextercioby said:The proof goes directly by putting cos a = Re (e^ia).
ainster31 said:According to definition 12.1.3, a set of real-valued functions can be proven to be orthogonal if (φm, φn) = 0. So why is it necessary to prove (φ0, φn) = 0?
ainster31 said:So you're saying it was unnecessary?[...]