guyvsdcsniper
- 264
- 37
- Homework Statement
- Prove the commutator relation [H,a*]=hwa*
- Relevant Equations
- [H,a*]=hwa*
I am going through my class notes and trying to prove the middle commutator relation,
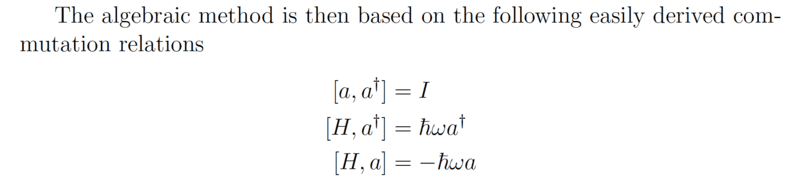
I am ending up with a negative sign in my work. It comes from [a†,a] being invoked during the commutation. I obviously need [a,a†] to appear instead.
Why am I getting [a†,a] instead of [a,a†]?
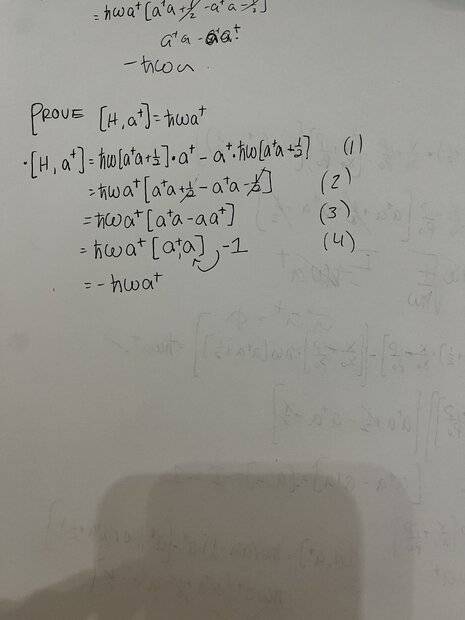
I am ending up with a negative sign in my work. It comes from [a†,a] being invoked during the commutation. I obviously need [a,a†] to appear instead.
Why am I getting [a†,a] instead of [a,a†]?