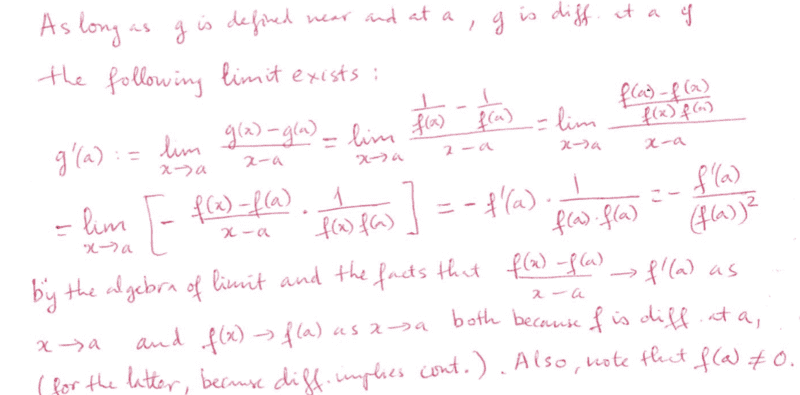SUMMARY
The discussion centers on proving the differentiability of a function using its definition, specifically addressing the assumption that the derivative exists at a point. The key equation referenced is the limit definition of the derivative, ##f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a}##. The assumption of differentiability is justified by the initial condition stating that the function ##f## is differentiable. This foundational understanding is crucial for correctly applying the limit definition in calculus.
PREREQUISITES
- Understanding of the limit definition of a derivative
- Familiarity with differentiable functions
- Basic knowledge of calculus concepts
- Ability to manipulate mathematical expressions
NEXT STEPS
- Study the formal definition of differentiability in calculus
- Explore examples of differentiable and non-differentiable functions
- Learn about the implications of differentiability on continuity
- Investigate the application of the Mean Value Theorem
USEFUL FOR
Students studying calculus, mathematics educators, and anyone seeking to deepen their understanding of differentiability and its implications in mathematical analysis.