Proving Quadrilateral Diagonal as Circle Diameter

  • Thread starter Thread starter mr.physics
  • Start date Start date
  • Tags Tags
    Proof
AI Thread Summary
A quadrilateral with sides measuring 39, 52, 60, and 25 is inscribed in a circle, leading to the challenge of proving that one of its diagonals is a diameter. This proof is linked to Thales' Theorem, which states that if a triangle is inscribed in a circle, the angle subtended by the diameter is a right angle. Despite the promise of extra credit, neither the teacher nor the students were able to solve the problem initially. An illustration was provided to aid understanding, but the full solution was later redacted from the discussion. The topic highlights the intersection of geometry and theorems in proving properties of cyclic quadrilaterals.
mr.physics
Messages
21
Reaction score
0
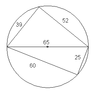
Here is a proof my math teacher gave us a while ago. He offered an enormous number of extra credit points if someone could solve it but no one did. We later asked him for the solution and he admitted that he could not solve it either. And here it is:

A quadrilateral whose consecutive sides have lengths 39, 52, 60 and 25 respectively, is inscribed in a circle. Prove that one of the diagonals of the quadrilateral is a diameter of the circle.
 
Physics news on Phys.org
This is a consequence of Thales' Theorem.


[Full solution snipped]

See the accompanying illustration for motivation.


--Elucidus

EDIT: I just realized this is in Homework Questions. My apologies. I have redacted the solution.
 

Attachments

  • Quadrilateral.gif
    Quadrilateral.gif
    1.7 KB · Views: 454
Last edited:

Thread 'Family of lines that are at a distance of 5 from the origin'

I picked up this problem from the Schaum's series book titled "College Mathematics" by Ayres/Schmidt. It is a solved problem in the book. But what surprised me was that the solution to this problem was given in one line without any explanation. I could, therefore, not understand how the given one-line solution was reached. The one-line solution in the book says: The equation is ##x \cos{\omega} +y \sin{\omega} - 5 = 0##, ##\omega## being the parameter. From my side, the only thing I could...
View full post »

Thread 'Making the denominator of a certain fraction real'

Essentially I just have this problem that I'm stuck on, on a sheet about complex numbers: Show that, for ##|r|<1,## $$1+r\cos(x)+r^2\cos(2x)+r^3\cos(3x)...=\frac{1-r\cos(x)}{1-2r\cos(x)+r^2}$$ My first thought was to express it as a geometric series, where the real part of the sum of the series would be the series you see above: $$1+re^{ix}+r^2e^{2ix}+r^3e^{3ix}...$$ The sum of this series is just: $$\frac{(re^{ix})^n-1}{re^{ix} - 1}$$ I'm having some trouble trying to figure out what to...
View full post »

Similar threads

MHB Quadrilateral Circumscribed Circle Diagonals and Chords Concurrency Proof
Replies
1
Views
1K
Similar Triangles Formed by Diagonals of Quadrilateral in Circle
Replies
1
Views
5K
(Rigorously) Prove that two medians of a triangle intersect
Replies
2
Views
3K
MHB Find the diameter of a circle given linear velocity?
Replies
5
Views
3K
An algebraic proof that a convex quadrilateral has intersecting diagonals
Replies
4
Views
7K
Proving Equal Diagonals in a Quadrilateral Inscribed in a Circle
Replies
16
Views
3K
Vector proof of generalized parallelogram law for quadrilaterals
Replies
6
Views
11K
Proving Parallelogram PQRS & Quadrilateral ABCD: Help Needed
Replies
6
Views
12K
Cantor's Diagonalization Proof of the uncountability of the real numbers
2
Replies
93
Views
20K
Need some math help very difficult problems
Replies
9
Views
4K

Hot Threads

Recent Insights

Back
Top