Pulley and weights hanging from spring balance

[rudransh verma]

Homework Statement

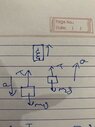
In the fig, a smooth pulley of negligible weight is suspended by a spring balance. Weights of 1kg and 5kg are attached to the opposite ends of a string passing over the pulley and move with acceleration because of gravity. During their motion the spring balance read a weight of ?

Relevant Equations

$F=ma$

Net force acting downwards is $5g-g=4g$ in downward direction. Net force on pulley is $2T-4g$. Weight measured by balance?

 

[Lnewqban]

What do you think?
Same measurement when bodies are released and when accelerating?
I believe that is what the question is about.

The problem is treating kg as unit of force, when it is a unit of mass.
The spring scale can only measure force; therefore, its markings should be kg-force.

https://courses.lumenlearning.com/physics/chapter/9-3-stability/

Your calculations without a free body diagram seem not to be accurate.
The best you can, please draw a FBD for the system of spring scale/masses, not including internal forces (especially T).

 

[Doc Al]

Net force acting downwards is $5g-g=4g$ in downward direction. Net force on pulley is $2T-4g$. Weight measured by balance?

The only thing pulling down on the pulley is the string. The weights of the masses act on the masses, not on the pulley.

 

[rudransh verma]

https://courses.lumenlearning.com/physics/chapter/9-3-stability/

"Figure 7. (a) here we see neutral equilibrium. The cg of a sphere on a flat surface lies directly above the point of support, independent of the position on the surface. The sphere is therefore in equilibrium in any location, and if displaced, it will remain put. (b) Because it has a circular cross section, the pencil is in neutral equilibrium for displacements perpendicular to its length."

I don't know why you put this link here but I was stuck on neutral equilibrium. The sphere is always in neutral equilibrium since in whatever position we place the sphere there is no top and bottom of the sphere. It can never fall. Right?

 

[rudransh verma]

Your calculations without a free body diagram seem not to be accurate.
The best you can, please draw a FBD for the system of spring scale/masses, not including internal forces (especially T).

I cannot make a very good FBD. I think the balance will measure less weight than 6 kg, either 5kg or 4kg because the net force on 1kg mass is upwards due to which balance may not measure full 1kg weight. So it will surely be less than 6kg. But I can’t prove it.

 

[Doc Al]

Don't "do it in your head" or guess. You have free body diagrams for the masses, now add one for the pulley.

Analyzing forces on the masses will allow you to solve for the acceleration and the tension.

 

[Lnewqban]

"Figure 7. (a) here we see neutral equilibrium. The cg of a sphere on a flat surface lies directly above the point of support, independent of the position on the surface. The sphere is therefore in equilibrium in any location, and if displaced, it will remain put. (b) Because it has a circular cross section, the pencil is in neutral equilibrium for displacements perpendicular to its length."

I don't know why you put this link here but I was stuck on neutral equilibrium. The sphere is always in neutral equilibrium since in whatever position we place the sphere there is no top and bottom of the sphere. It can never fall. Right?

If the center of mass of the body or system of bodies has freedom to occupy a lower position closer to ground (using its potential energy to move), it will.
For the sphere rolling on a flat surface is impossible.
For the system of bodies of this problem, it is possible.

 

[Steve4Physics]

Calculating the spring-balance reading will be a valuable exercise for the OP and I would encourage this.

But it is worth noting that choosing from the list of possible answers requires no calculations (other than 1+5=6).

First realize that the centre of gravity of the pulley+masses accelerates downwards. Finding the allowed range of the upward force (from the spring) is then simple.

On a different point, the spring could be changing length, e.g. if oscillations occur. But (arguably) the wording of the original question precludes this.

 

[rudransh verma]

Don't "do it in your head" or guess. You have free body diagrams for the masses, now add one for the pulley.

Analyzing forces on the masses will allow you to solve for the acceleration and the tension.

The problem is treating kg as unit of force, when it is a unit of mass.
The spring scale can only measure force; therefore, its markings should be kg-force.

The question asks about the weight and gives options in kg. I think it is asking the kg force
When I calculated and taking g=10 I got a=6.67 m/s^2. So if we treat the bodies as one 6kg and the acceleration as a=6.67 m/s^2 then the force acting downwards and on the balance is F=40.02 N. That's what the balance measures. Balance measures 4 kg.