Pulley on a moving base problem

[AliGh]

Hi today the teacher showed us analyzing forces in a system he showed them on easy problems
But at the end of the class he gave us this question to solve
Its not homework because its way beyond what he taught
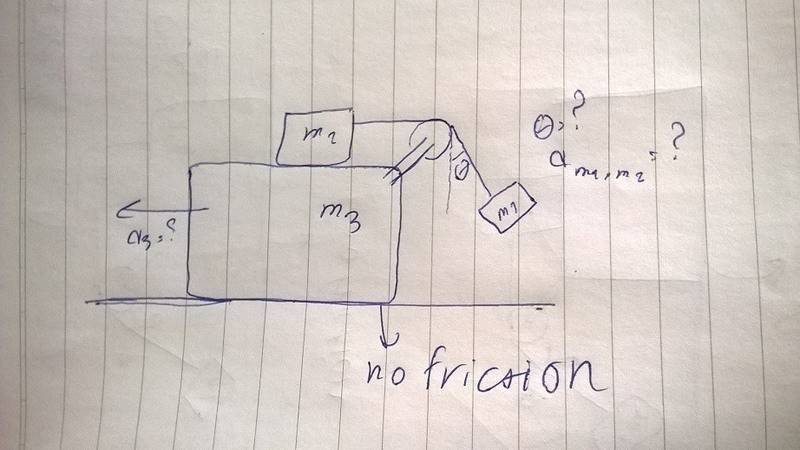
The base moves without friction on surface
So i want to find a3 and theta and a of 2 and 1
How should i do this ? Where should i start from ?

 

[Perq]

Find a2, by calculating the force that m1 will pull the line with.
(I assume no friction between m3 and m2 too) From momentum conservation, calculate a3. (m2v2 + m3a3 = 0 in any given moment)

Theta will be pretty much cosine of a1 (assuming it is vertical) and a3

 

[AliGh]

Find a2, by calculating the force that m1 will pull the line with.
(I assume no friction between m3 and m2 too) From momentum conservation, calculate a3. (m2v2 + m3a3 = 0 in any given moment)

Theta will be pretty much cosine of a1 and a3

I think theta is for when the base is moving not while we haven't released m2
And no friction between m2 and m3

 

[Perq]

You need to connect them, in one equation, so when you calculate a2 (from a1), you also connect it to possible theta from a3, because theta will affect your a1.

 

[AliGh]

You need to connect them, in one equation, so when you calculate a2 (from a1), you also connect it to possible theta from a3, because theta will affect your a1.

I think theta here is depended on m1 , m2 and m3 ... it is solvable , but not the way the teacher taught us to the problems were very simple compared to this

 

[Perq]

You need to create two equations, and solve them like that (unless you don't know how to, mathematically). And, yes, masses are important, because you need to calculate it using forces, but what you are really interested in here are accelerations.

 

[nasu]

Do you have the full text of the problem?
Is the drawing done for the initial position of the system?
Are the acceleration required for this initial position?

 

[AliGh]

Do you have the full text of the problem?
Is the drawing done for the initial position of the system?
Are the acceleration required for this initial position?

There is no text he just drew it .. no drawing of initial position and accelerations are not required
I found a way ... got sin(theta) = m2 / (2*m2+1) i don't know if currect or not (it seems odd that its only depended on m2)

 

[nasu]

If you don't know the initial condition, how can you "find" that angle? What is the meaning of it? All three bodies mat move and the angle will depend on time.

 

[AliGh]

If you don't know the initial condition, how can you "find" that angle? What is the meaning of it? All three bodies mat move and the angle will depend on time.

So your saying that if initial angle was 0 it will going to change until m1 hits the ground ? wouldn't it become constant after some time passed ? And can you prove it ?

 

[nasu]

I said that if it's some value, as shown there, it will change.
Probably it will change even if it's initially zero.
To prove what?

 

[AliGh]

I said that if it's some value, as shown there, it will change.
Probably it will change even if it's initially zero.
To prove what?

That it will change forever

 

[Perq]

It took me a little while to understand how it would look like at t=0, but this does make sense.
You should have drawn it at t=0. :P Draw as it is draw, it suggest that theta(t) with t=0 isn't 0. :V

 

[haruspex]

m2v2 + m3a3 = 0

Did you mean that? It mixes momentum with force.

Theta will be pretty much cosine of a1 (assuming it is vertical) and a3

a1 would not be vertical, and I assume you mean cos(theta) will be a ratio of the accelerations.

the angle will depend on time.

At first I though we are just to find the instantaneous acceleration when at angle theta. If theta is to be 'found', I can only suggest it is asking for the maximum theta if it starts at theta=0.
There may be an easier way, but it took me a page of algebra (no solving differential equations) to find max sin(theta) as a function of $m_3(\frac 1{m_1}+\frac 1{m_2})$

Correction: I was not able to find the max theta. What I found was the theta at which $\dot{\theta}$ is maximised.

 

[AliGh]

Did you mean that? It mixes momentum with force.

a1 would not be vertical, and I assume you mean cos(theta) will be a ratio of the accelerations.
At first I though we are just to find the instantaneous acceleration when at angle theta. If theta is to be 'found', I can only suggest it is asking for the maximum theta if it starts at theta=0.
There may be an easier way, but it took me a page of algebra (no solving differential equations) to find max sin(theta) as a function of $m_3(\frac 1{m_1}+\frac 1{m_2})$

Correction: I was not able to find the max theta. What I found was the theta at which $\dot{\theta}$ is maximised.

The next session he came and said that he will give us points if we solve this. I don't think he himself has solved it ..
I think i should prove that theta would be variable no matter what starting theta we have to show that problem asks for a wrong thing

 

[Perq]

Did you mean that? It mixes momentum with force.

No, m2v2 is momentum, and m3v3 is momentum. I'm not mixing forces with momentum. You that equation to calculate (I believe) the speed (and acceleration) of block 3. (you might also need to add m1v1, as they are on the "static" side).

With vertical, I meant m1 being "vertical". :P Not the acceleration. Sorry for the confusion. Yeah, exactly that. :P

Theta is to be found, for sure.

Process will go something like this:
m1 pulls m2 down, when at t=0, theta=0.
m2 starts moving, and because of conservation of momentum, m3 starts moving the other way (namely, left).
because m3 started moving left, m1 starts to tilt right (is this the correct word - haven't used this kind of English for years x__x) to angle theta_max, which is to be determined.

Because of that, I doubt that this is that easy, because when m1 tilts, the force m1 pulls m2 will also increase, meaning the whole process needs to be repeated (which means differentials are needed here).

 

[haruspex]

No, m2v2 is momentum, and m3v3 is momentum..

But you wrote a3, not v3.

to angle theta_max, which is to be determined.

Well, it doesn't say we're to find the max theta (taking initial state to be theta=0), that was just one interpretation. But I now think it more likely the idea is to find the steady state (insofar as an accelerating system can be said to be steady state) theta, which is not the same thing. Since that would have $\ddot{\theta}=0$, it would be the solution I mentioned in post #14 (assuming my algebra is right).

 

[Perq]

Ye, steady state makes more sense, sorry for my mis-wording. :P

m3a3 was of course a mistake - didn't notice it. :P Sorry, again.

If acceleration is constant, you can somewhat say it is "steady", at least theta would remain steady.