Pulley system to balance the weight of a person

[lorenz0]

Homework Statement

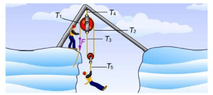
If the mass of the man to be saved is $m$, the mass of the smaller pulley $m_p$ and the mass of the bigger pulley $M_p$, find: $T_1, T_2, T_3, T_4, T_5, F.$

Relevant Equations

$\vec{F}=m\vec{a}$

Since we are dealing with an ideal rope, we have that $T_1=T_2=T_3=F and T_2+T_3=2F=(m+m_p)g\Leftrightarrow F=\frac{m+m_p}{2}g.$
$T_4=3F+(m+m_p+M_p)g=\frac{3}{2}(m+m_p)g+(m+m_p+M_p)g=(\frac{5}{2}m+\frac{5}{2}m_p+M_p)g$ and $T_5=mg-2F.$

Is this correct? If not, I woould appreciate a brief explanation on how to deal with these ideal-pulley ideal-rope systems since they seem quite counterintuitive to me.

 

[jbriggs444]

I agree that $T_1 = T_2 = T_3$ and that we can call this $F$. As you say, the pulleys are ideal so all three tensions will match.

I agree that $T_2 + T_3 = 2F$. Since those two tensions support the man plus the smaller pulley, it follows that $2F = (m+m_p)g$. So yes, we can conclude that $F=\frac{m+m_p}{2}g$

You will have to persuade me that $T_4 = 3F + (m + m_p + M_p)g$. How did you arrive at that? I think you are double dipping there.

 

[Steve4Physics]

@lorenz0, in addition to what @jbriggs444 has said, can I add this...

Presumably the system is in equilibrium (acceleration = 0).

Your equations/logic could be clearer if not joined together into a single line/paragraph.

The facts that $T_1 = T_2 = T_3$ and $T_2+T_3=2F$ lead to $T_1 = F$. Can you see a simpler way to get this relationship directly?

All parts of the system are in equilibrium. You can draw a free body diagram for any part of the system. If you draw (or just imagine) a free body diagram for the upper pulley alone, it should help you.

 

[lorenz0]

@lorenz0, in addition to what @jbriggs444 has said, can I add this...

Presumably the system is in equilibrium (acceleration = 0).

Your equations/logic could be clearer if not joined together into a single line/paragraph.

The facts that $T_1 = T_2 = T_3$ and $T_2+T_3=2F$ lead to $T_1 = F$. Can you see a simpler way to get this relationship directly?

All parts of the system are in equilibrium. You can draw a free body diagram for any part of the system. If you draw (or just imagine) a free body diagram for the upper pulley alone, it should help you.

Drawing the free body diagram for the upper pulley alone, it seems that $T_4=3F+M_Pg.$ Is this correct?

 

[jbriggs444]

Drawing the free body diagram for the upper pulley alone, it seems that $T_4=3F.$ Is this correct?

No. You missed something this time.

 

[lorenz0]

No. You missed something this time.

The mass of the upper pulley, I guess.

 

[Lnewqban]

Drawing the free body diagram for the upper pulley alone, it seems that $T_4=3F.$ Is this correct?

 

[Steve4Physics]

The mass of the upper pulley, I guess.

You mean the weight of the upper pulley. (Hopefully it's not a 'guess', as a free body diagram must include the body's weight.) Your Post #4 edited equation is now correct.

BTW, it's best to not significantly edit a post once someone has replied to it. Better to write a new Post making clear any changes you want. That can avoid confusion and messages at cross-purposes.