Pulleys and Springs: Really stupid question

[Saladsamurai]

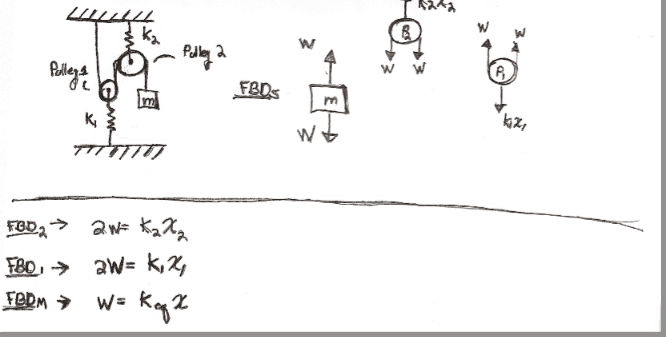
So I am trying to follow along this example in the text to find k_eq of the system.

I can follow everything up until the point that they say: "It follows that x=2(x₁+x₂)

where:

x = displacement of mass
x₁ =displacement of Pulley1_cm
x₂ =displacement of Pulley2_cm

I am not seeing it. I am also very tired. So please help me and then slap me

 

[rl.bhat]

For the time being, suppose k2 is not operating. When the pulley1 moves up through x1, what is the distance moved by the mass ?

 

[Saladsamurai]

Yeah. I don't see it. How ca I relate anything to x?

Like rl.bhat says: If k2 was not operating, I know that 2W=k1*x1 ... but I
don't see how that helps?

 

[Saladsamurai]

Anyone?

 

[rl.bhat]

Just compare the movement of the pulley and release of the rope at mass end.
When the pulley1 moves through x1, mass moves through y1 distance ,then y1 = 2x1. Similarly for pulley 2, y2 = 2x2. So the distance moved by the mass y1 + y2 = x = 2(x1 + x2)

 

[Saladsamurai]

Okay. I mean, I believe you. I just don't see it.

 

[rl.bhat]

Okay. I mean, I believe you. I just don't see it.

When p1 moves up through x1, on both side of the pulley x1 rope is released. That adds up to 2x1.

 

[Saladsamurai]

When p1 moves up through x1, on both side of the pulley x1 rope is released. That adds up to 2x1.

Ahh. I think I see it now. Thanks for your patience!