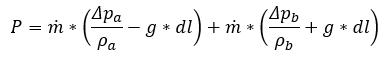Pumping power calculation of a vertical closed-loop system

[argeus]

TL;DR Summary

pumping power calculation of a vertical closed-loop system assuming the hydrostatic term

Hi there,
I hope that somebody can help me with this.. Any response is much appreciated!

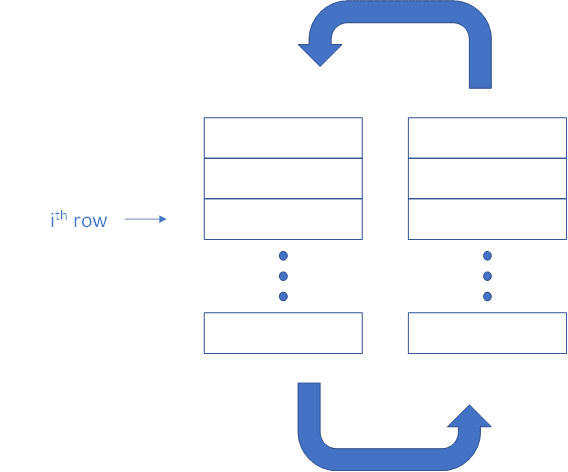
Let's have a vertical closed-loop system where the fluid circulates using the pump. The temperature in both sections gradually changes (the upcomer section is heated up) so that the densities, velocities, and pressure drop change as well. Hence, it would be beneficial to split the geometry into horizontal sections; each section (downcomer and upcomer) is divided into a certain number of elements, each of the same height. The point is to calculate the pumping power needed for fluid circulation. The total power is calculated per partes, i.e. for each i^th row separately and then simply summed together.

For any single i^th row, the pumping power equation (w/o hydrostatic term) yields:

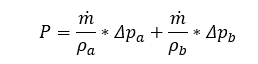
Note that subscript a refers to a downcomer and subscript b to an upcomer, respectively. Symbol m refers to the mass flow rate, ρ is density and Δp is the pressure drop across the element in the i^th row as per Darcy friction eq.
Now assuming a hydrostatic pressure due to the changing density, one gets:

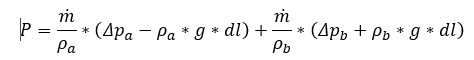
Simply, g denotes gravitational acceleration, and the term dl refers to the height of the element in the i^th row.
Rearranging a bit:

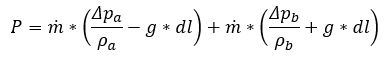
Since the mass flow is the same in both channels, we finally get:

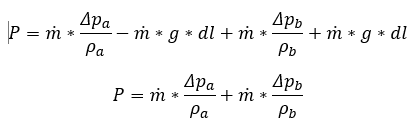
Does this mean that the pumping power is independent of the hydrostatic pressure in the closed loop even when the fluid densities in both vertical channels differ? This does not seems correct to me, however, simply cannot find where I'm going wrong..

 

[Lnewqban]

Welcome @argeus !
Pumping required power depends only on fluid flow and pressure differential between inlet and outlet of the pump.

 

[jack action]

Does this mean that the pumping power is independent of the hydrostatic pressure in the closed loop even when the fluid densities in both vertical channels differ?

Rewriting your equation:
$$P = \rho_a \dot{V}_a\frac{\Delta P_a}{\rho_a} + \rho_b \dot{V}_b\frac{\Delta P_b}{\rho_b}$$
Where $\rho_a \dot{V}_a = \rho_b \dot{V}_b =\dot{m}$. Simplifying:
$$P = \dot{V}_a\Delta P_a + \dot{V}_b\Delta P_b$$

 

[argeus]

Dear Lnewqban,

Thank you for your reply. This is completely true and it matches the first eq. However, the question of how the pressure differential should be calculated remains open. I would guess that it consists of two terms, i.e. frictional forces and hydrostatic forces. If the temperature in the upcomer section is higher (because this section is heated), the density decreases and the hydrostatic balance should promote fluid flow. This is how thermosiphons (aka heat pipes) work. In a specific case, the hydrostatic force difference could balance the frictional forces so that a natural circulation in the closed-loop system is established and no pump is needed. For instance, the geometrical integrity of the Trans-Alaska Pipeline System in a permafrost environment is maintained using such heat pipes. So neglecting the hydrostatic term indicates to me that I've just overlooked something..

 

[Lnewqban]

That difference of temperatures, if substantial and continuous due to good heat transfer on both halves of the loop, may help your pump.
If most thermal energy does not remain in the fluid, something else is needed to stablish and keep a flow, overcoming friction and turbulence.
There is phase change in a heat pipe, you don’t have that in your system.

Nevertheless, at start up, that T differential may not be there, and your pump will need to have increased power to overcome friction of the system at an intermediate temperature.

If you have valves, expansion tanks, aireators, thermometers, coils, etc. in your loop, you will need to calculate pump power for worst conditions (full flow and restricted flow with all closed valves, restricted coils, air pockets traped in horizontal pipes, etc.).
Therefore, a safety factor should be included in your calculations as well.