bluesteels
- 28
- 1
- Homework Statement
- The idealized cycle shown is known as the Otto cycle. (Figure 1)Suppose an engine is executing this Otto cycle, using a gas (not necessarily ideal) as its working substance. From state A to state B, the gas is allowed to expand adiabatically. (An adiabatic process is one in which no heat is added to, or given off by, the working gas.) The gas is then cooled at constant volume until it reaches state C, at which point it is adiabatically compressed to state D. Finally, it is heated at constant volume until it returns to state A.
- Relevant Equations
- adiabactic delta u = -w
isothermal Q=W
Figure 1:
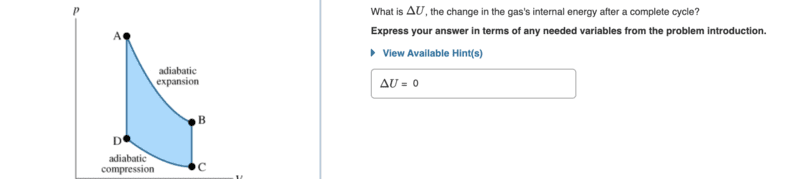
im so confused on why is the internal energy not zero for the 2nd picture because i thought if the gas returning to its original states so it zero
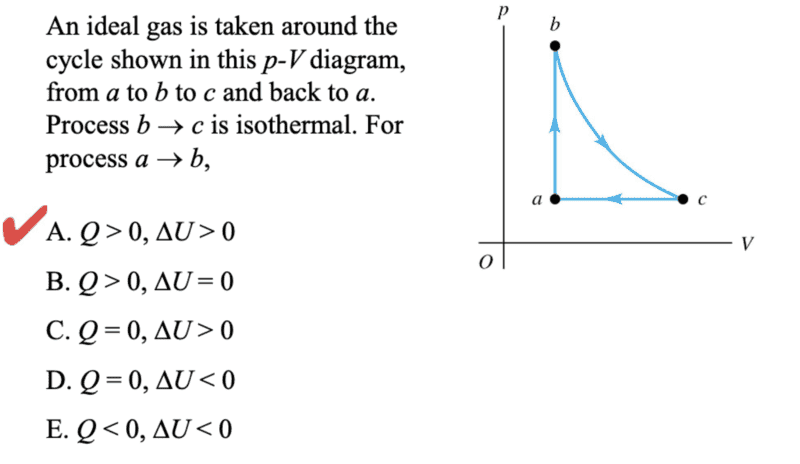
im so confused on why is the internal energy not zero for the 2nd picture because i thought if the gas returning to its original states so it zero