penroseandpaper
- 21
- 0
- Homework Statement
- Please see screenshot
- Relevant Equations
- Please see screenshot
Hi all,
I've been trying to follow a question I came across on a website. And I'm able to understand everything up until the separation of variables for solving the differential equation and coming to a solution with arctan. But there are a few things that aren't explained that I was hoping somebody could shed some light on.
Right, so first, it's to do with an object that is projected upwards and has initial velocity greater than zero. Applying Newton's second law, the left hand side is m dv/dt and the left hand side has W+R; it's the quadratic expression for air resistance. Motion is upwards, and both forces act opposite (down). Dividing through by m leads to the differential equation found in the screenshots below.
Separation of variables means we can move the right hand side to the left (making it the denominator, under 1). And that can be integrated to result in the expression with arctan. Meanwhile, t is the result of integration on the right hand side. That's where I got up to without issue.
My first question is what happens to the constant of integration? I'm not exactly sure how to confirm if it has a value, given initial velocity is greater than zero. I know t=0 at this time, but I'm in a bit of a fuzz trying to balance the sides.
Second, why does the sign change at the top of the motion when v=0? Is that to do with changing the order of the boundaries?
And finally, why is time to the top of the motion equal to the positive solution of the integrand, with v0 in place of v?
Thank you for your help,
Penn


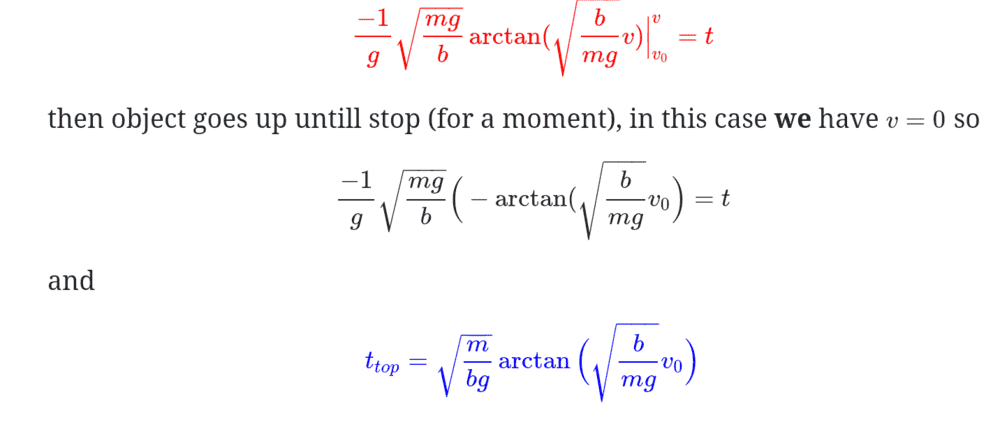
I've been trying to follow a question I came across on a website. And I'm able to understand everything up until the separation of variables for solving the differential equation and coming to a solution with arctan. But there are a few things that aren't explained that I was hoping somebody could shed some light on.
Right, so first, it's to do with an object that is projected upwards and has initial velocity greater than zero. Applying Newton's second law, the left hand side is m dv/dt and the left hand side has W+R; it's the quadratic expression for air resistance. Motion is upwards, and both forces act opposite (down). Dividing through by m leads to the differential equation found in the screenshots below.
Separation of variables means we can move the right hand side to the left (making it the denominator, under 1). And that can be integrated to result in the expression with arctan. Meanwhile, t is the result of integration on the right hand side. That's where I got up to without issue.
My first question is what happens to the constant of integration? I'm not exactly sure how to confirm if it has a value, given initial velocity is greater than zero. I know t=0 at this time, but I'm in a bit of a fuzz trying to balance the sides.
Second, why does the sign change at the top of the motion when v=0? Is that to do with changing the order of the boundaries?
And finally, why is time to the top of the motion equal to the positive solution of the integrand, with v0 in place of v?
Thank you for your help,
Penn