Quadratic equation and its roots

[kshitij]

Homework Statement

What are the roots of the equation x=1+1/x?

Relevant Equations

x=(-b±√(b²-4ac))/(2a),
when ax^2+bx+c=0

On simplifying the given equation we get, x^2-x-1=0 and using the quadratic formula we get x=(1+√5)/2 and x=(1-√5)/2
Now, as the formula suggests, there are two possible values for x which satisfies the given equation.

But now, if we follow a process in any general calculator by entering
1+1/Ans
into the calculator repeatedly, we always reach this particular number as shown,

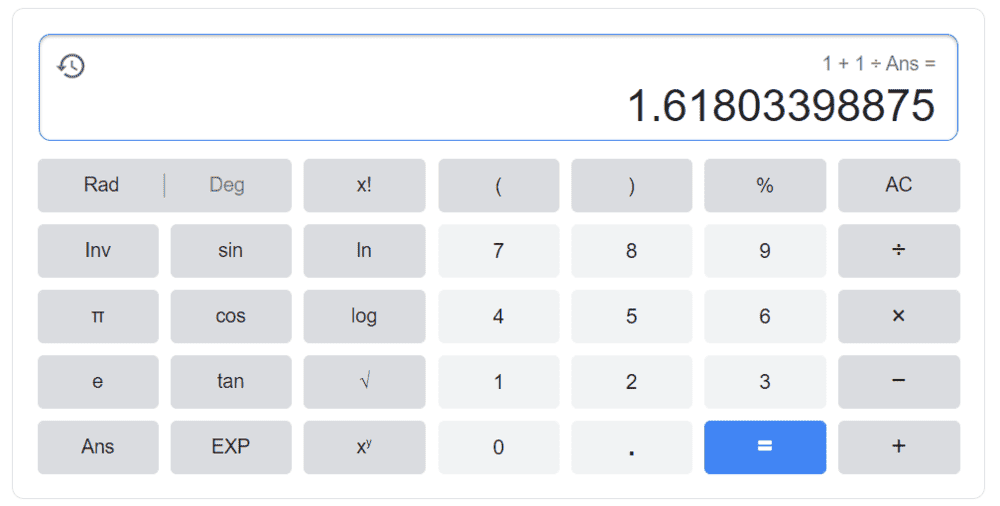
Now obviously we cannot do this process for when the value of Ans is set to 0.
But other than that, no matter what the value of answer we choose,
for all real numbers if we repeatedly do this process on any calculator,
we always reach the above mentioned number.

This still somehow makes sense to me because if we are repeating our input into the equation 1+1/Ans
what we are actually doing looks somewhat like this,
Ans=1+1/Ans
here Ans is variable

So we eventually did end up with our starting equation whose roots were,
(1+√5)/2 and (1-√5)/2
And the number which the calculator shows is also equal to (1+√5)/2 But my question is why do we end up always at (1+√5)/2 and and never on (1-√5)/2?
x=(1-√5)/2 also satisfies the original equation so why does the calculator never show us the other root of this equation?

Now this got me thinking and I tried to manipulate the original equation to something like this (don't ask me why I did this cause even I don't know that, I was just playing around with random inputs like these when the result for this input surprised me),
x=1/(x-1)
This equation is exactly same as our original equation with the only difference being that in the original equation we cannot have the value of x as 0 and in the modified version, x should not be equal to 1. So now let's do another process (repeatedly) in the calculator,
1/(Ans-1)

again by the same logic we can see that the process which we are doing, actually looks like the equation,
Ans=1/(Ans-1)
Only difference this time is that now we cannot set the value of answer as 1 or 2.
Other than that, for all real values of Ans, this time we reach this particular number,

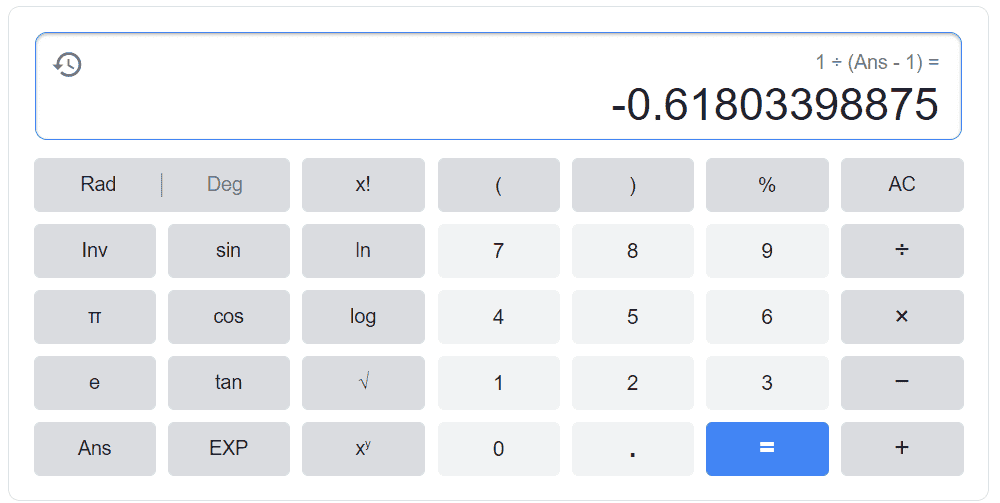
And this number is exactly equal to the other value of x in our original equation which is (1-√5)/2

So that is my question, why does the calculator have a favorite root for a particular function when more than one values satisfy the equation?
If both the roots are equivalent, then half of the times we should have reached (1+√5)/2 and other half of the times (1-√5)/2 randomly.

Also this isn't some usual homework question, I didn't knew whom to ask this question so I posted it here. I hope it doesn't break any rules.

 

[BvU]

Hi,

But now, if we follow a process in any general calculator by entering
1+1/Ans
into the calculator repeatedly, we always reach this particular number as shown,

But other than that, no matter what the value of answer we choose,
for all real numbers if we repeatedly do this process on any calculator,
we always reach the above mentioned number.

You want to be careful with generalizations.

Basically what you are doing is you solve x = x + 1/x by a well-known procedure called successive substitution: you solve x = f(x) by starting at some x₀ and calculating f(x₀). This result is your next guess, x₁ and you calculate x₂=f(x₁).
Etc. until your x doesn't change any more.

Example:
x₀ = 3
x₁ = 1.333
x₂ = 1.747
x₃ = 1.571 etc converging to (1+√5)/2

and sure enough, x₀ = -3 brings you to the same point.
BUT do you see which starting values take you to the alternative solution ?

Hint: It's only a small range. But your generalization 'no matter what the value of answer we choose' is definitely incorrect !

Advanced question: can you also see what kind of functions/starting value will not converge with this method ?

Also this isn't some usual homework question, I didn't knew whom to ask this question so I posted it here. I hope it doesn't break any rules.

It is a very good and clear question!

 

[BvU]

Here you see the situation for x = 1/(x-1)

Again: can you find which starting values take you to the alternative solution ?

If both the roots are equivalent, then half of the times we should have reached (1+√5)/2 and other half of the times (1-√5)/2 randomly.

Conclusion: both roots are almost never equivalent (never say never unless you're sure)

$\$

 

[kshitij]

can you find which starting values take you to the alternative solution ?

It looks like,
for the first graph only the input (1-√5)/2 will get us to the alternate solution,
and similarly for the second graph only (1+√5)/2 gives us exactly the intersection between the lines y=x and y=1/(x-1),
anything other than that seems to slowly-slowly move away from (1+√5)/2.
That's when I tried to manually trace straight lines on the given graphs. So, I'm not sure but when I was trying this process on the calculator I did end up on the alternate solution every-time I started with the alternate solution.

edit: I will surely try this on GeoGebra as well.

 

[kshitij]

can you also see what kind of functions/starting value will not converge with this method ?

I can obviously see that when you get close to an asymptote (x=0 in the first graph and x=1 in the second), it will not converge. Now what are the possible inputs that will reach to an asymptote, that I'm not sure about.

Obviously starting on an asymptote surely doesn't converge, but there are other values too (e.g- x=2,1.5 in the second graph) that ends up on an asymptote, But I don't how to find them. I'll think about it.

edit: I think I found a pattern to reach an asymptote,
lets talk about the second equation (because this method doesn't work for the first equation)
y=1/(x-1)
we just solve for the values of x where the equation gives us y=1
i.e., 1/(x-1)=1
which gives x=2,

Now again if we find some input which will give 2 as output, the function will not converge as 2 will again give us back 1 as output.
so,
1/(x-1)=2
which gives x=3/2

Similarly, we can find lots of values namely,
x=1,2,3/2,5/3,8/5,13/8...

Also I spotted something pretty cool,
these values of x's are the ratios of consecutive Fibonacci numbers!
Which is cool because I've heard that the ratio of consecutive Fibonacci numbers approaches the golden ratio!
the golden ratio is basically our solution (1+√5)/2

This is crazy because if we start with the golden ratio then it converges again!

Here's a gif where I plotted few of these values of x

 

[kshitij]

Here you see the situation for x = 1/(x-1)

View attachment 277816
Again: can you find which starting values take you to the alternative solution ?

Conclusion: both roots are almost never equivalent (never say never unless you're sure)

$\$

I almost forgot to thank you for your wonderful response! Those graphs do help a lot to understand the problem.

 

[BvU]

only the input (1-√5)/2 will get us to the alternate solution

You are absolutely right !

Bad on my part (shouldn't do this off the top of my head).
Has to do with the slope of f(x) -- more googling (or diving into the books ) required .
E.g section 7.5http://math.jbpub.com/numericalmethods/pdf/Linz07.pdf

 

[kshitij]

You are absolutely right !

Bad on my part (shouldn't do this off the top of my head).
Has to do with the slope of f(x) -- more googling (or diving into the books ) required .
E.g section 7.5http://math.jbpub.com/numericalmethods/pdf/Linz07.pdf

I think this video is relevant here

 

[Chestermiller]

This iterative method for solving x = f(x) will converge if there is a region around the root in which |f'(x)| < 1.

 

[kshitij]

This iterative method for solving x = f(x) will converge if there is a region around the root in which |f'(x)| < 1.

That is very interesting, in fact this video which I shared earlier also talks about how this has something to do with slopes.

But I can't quite get why is it so?

It somewhat feels like the concept of stable and unstable equilibrium in physics, where the root at which this function converges is at stable equilibrium and the other is unstable. This is just how I see it, but this doesn't explain why a region around the root in which |f'(x)| < 1 is the stable equilibrium position?

Also I have some other doubts as well.

I was plotting the same function by rearranging its terms, on GeoGebra, and pretty much everyone of them followed your rule

these above two were the original ones which I mentioned in the post,

And these two below were two similar cases which followed your rule,

I also found a few interesting cases as well like these below,

here we can see that,
|f'(x)| > 1 in the regions around both the roots,
so in these two cases our method should not work and it should not converge.

But there were some values for which our function didn't blow up to infinity, but instead it was dancing around two particular values.
Why is that happening?

Also my other question is,
can we have a function, for which |f'(x)| < 1 at regions around both the roots?
What will happen in this case? Will our function converge to both roots randomly?

Now I tried to guess one such function, but the one I found had some defects, it involved modulus and square roots,
$|y|= √ (x+1)$

So, for this I tried my process with two separate functions,
$y= √ (x+1)$ and $y= - √ (x+1)$

Now, this works for the one with positive sign but not for the one with negative sign, is this because of the square root which restricts our domain to only non-negative integers?

Anyway to sum it up,
1.) Why does our function converge if there is a region around the root in which |f'(x)| < 1?
2.) For functions in which |f'(x)| > 1 around both the roots, why are there some values for which f(x) ended up fluctuating between 2 particular values?
3.) Can we have a function where the regions around both the roots have |f'(x)| < 1? Will this function converge randomly to either of our roots in our process?

 

[BvU]

But I can't quite get why is it so?

Did the exposé on p 190 in the link I gave earlier not explain that clearly ?

 

[kshitij]

Did the exposé on p 190 in the link I gave earlier not explain that clearly ?

I actually didn't read that because when I started with section 7.5, a lot of stuff went over my head, I thought that I might have to read the whole thing from beginning or maybe my knowledge isn't enough to understand all of that, so I just saved that document for now.

I can still give it another try though.

 

[pasmith]

Start with a linear recurrence: By induction, you can show that the solution of $$a_{n+1} = \lambda a_n$$ is $$a_n = a_0\lambda^n$$. Now $|a_n| = |a_0||\lambda|^n$ is strictly decreasing if and only if $|\lambda|^{n+1} < |\lambda|^n$, ie. $|\lambda| < 1$.

Now consider the non-linear recurrence $$x_{n+1} = f(x_n)$$
Near a fixed point $x_0$ we can set $x_n = x_0 + \epsilon_n$ and expand $f(x_0 + \epsilon_n)$ in as a taylor series: $$x_0 + \epsilon_{n+1} = f(x_0) + \epsilon_nf'(x_0) + \cdots$$ Since $x_0 = f(x_0)$ this leaves $\epsilon_{n+1} \approx f'(0)\epsilon_n$. The linear theory tells us that $|\epsilon_n|$ will increase if $|f'(x_0)| > 1$ and decrease if $|f'(x_0)| < 1$. If $f'(x_0) = 1$ then this test is inconclusive.

 

[kshitij]

Start with a linear recurrence: By induction, you can show that the solution of $$a_{n+1} = \lambda a_n$$ is $$a_n = a_0\lambda^n$$. Now $|a_n| = |a_0||\lambda|^n$ is strictly decreasing if and only if $|\lambda|^{n+1} < |\lambda|^n$, ie. $|\lambda| < 1$.

Now consider the non-linear recurrence $$x_{n+1} = f(x_n)$$
Near a fixed point $x_0$ we can set $x_n = x_0 + \epsilon_n$ and expand $f(x_0 + \epsilon_n)$ in as a taylor series: $$x_0 + \epsilon_{n+1} = f(x_0) + \epsilon_nf'(x_0) + \cdots$$ Since $x_0 = f(x_0)$ this leaves $\epsilon_{n+1} \approx f'(0)\epsilon_n$. The linear theory tells us that $|\epsilon_n|$ will increase if $|f'(x_0)| > 1$ and decrease if $|f'(x_0)| < 1$. If $f'(x_0) = 1$ then this test is inconclusive.

I'm so sorry but this is beyond me. I thought that there must be some geometric way to see this through graphs, like the one in the first two responses by @BvU. I appreciate your efforts but I think this question is not for me (atleast not for now), But I do hope to understand this someday.

Thank you for your response.

 

[Chestermiller]

Suppose that the exact root is $x_E$. The recursion relationship being used is $$x^{n+1}=f(x^n)$$If we expand the right hand side in a Taylor series about $x_E$ and retain the linear terms, we obtain: $$x^{n+1}=f(x_E+x^n-x_E)=f(x_E)+f'(x_E)(x^n-x_E)$$From this it follows that $$(x^{n+1}-x_E)=f'(x_E)(x^n-x_E)$$and$$\frac{|x^{n+1}-x_E|}{|x^n-x_E|}=|f'(x_E)|$$So the magnitude of the deviation from the exact answer is getting smaler from one iteration to the next if the absolute value of the derivative of the function is less than unity at the root.