rwooduk
- 757
- 59
I'm having trouble understanding why the resistivity behaves as it does in comparison to the density of states for the quantum hall effect. Take the following two diagrams:
(A)
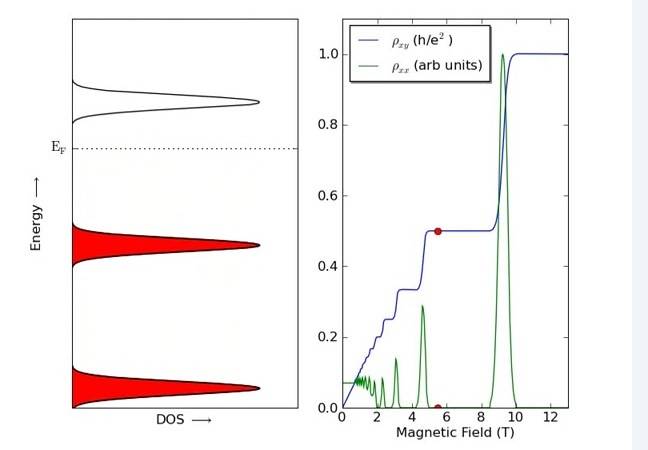
(B)
I understand that there can be no scattering in (A) because all states are full (i.e. no elastic) and the gap is too big to scatter inelastically. But why should the resistivity remain constant?
Also on (B) why does the resistivity increase when there are free states to scatter into? Is it saying scattering hinders conduction?
Having real trouble relating the DOS to resistivity. Any suggestions more than welcome.
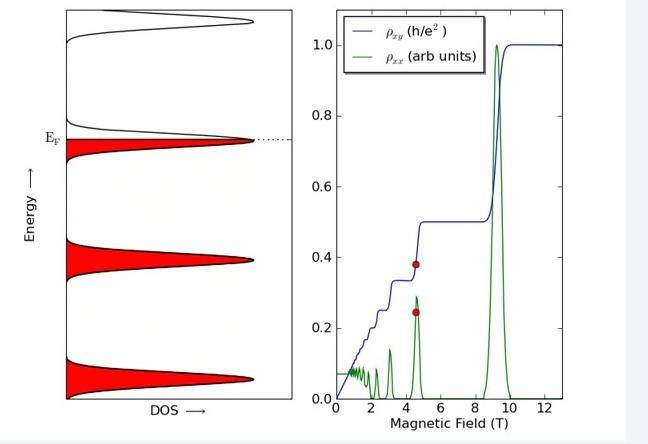
(A)
(B)
I understand that there can be no scattering in (A) because all states are full (i.e. no elastic) and the gap is too big to scatter inelastically. But why should the resistivity remain constant?
Also on (B) why does the resistivity increase when there are free states to scatter into? Is it saying scattering hinders conduction?
Having real trouble relating the DOS to resistivity. Any suggestions more than welcome.