Question about a figure in relativity textbook

[DocZaius]

Figure 2-4 in "Spacetime Physics" by Taylor & Wheeler

The figure illustrates the effects of free float on the perceived trajectory of a ball thrown in a room that is on a ledge and then in a room that is sawed free from the ledge.

In both cases, the ball is launched at the same speed and direction, and sprays ink on the side wall of the room. In all cases, the ball is thrown from right to left. Here is the illustration the book shows.

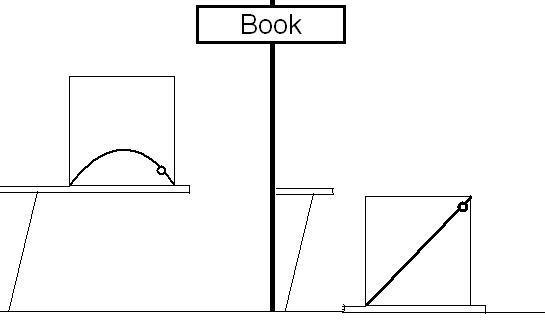
I have trouble with that illustration since it seems to me the ball would not make that ink trajectory in the free fall situation. To me it would seem to make this trajectory:

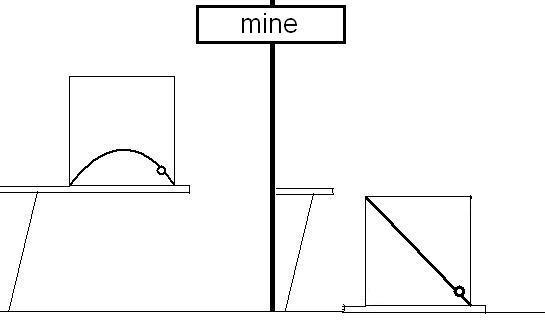
Can someone tell me why the book is right and I am wrong? To me it seems that once the ball is launched, it does not care if the house is free falling or not - it will arrive at the same spot relative to the stable side of the cliff. Why would it end up where the book says it does? Also, once the ball is launched in a free float situation, it seems it will behave as if having been launched int he same manner in the middle of space, and follow a straight line 45 degree angle trajectory to the opposite top corner of the room.

 

[Daverz]

In the right half of the second pic, you have the ball starting out in the upper left hand corner of the room at an angle of minus 45 degrees to the vertical. That can't be right as the two sides have to correspond at t=0, where the ball is in the lower left side of the room thrown at an angle of plus 45 degrees.

It might help to draw the positions of both the ball and the room at 1 second intervals. Note that the ball must follow the same trajectory in between the times where it's launched and where it hits the floor of the room, no matter what the room does, since there's no other force on the ball but gravity.

 

[DocZaius]

In the right half of the second pic, you have the ball starting out in the upper left hand corner of the room at an angle of minus 45 degrees to the vertical. That can't be right as the two sides have to correspond at t=0, where the ball is in the lower left side of the room thrown at an angle of plus 45 degrees.

It might help to draw the positions of both the ball and the room at 1 second intervals. Note that the ball must follow the same trajectory in between the times where it's launched and where it hits the floor of the room, no matter what the room does, since there's no other force on the ball but gravity.

In every diagram, the ball is thrown from the bottom right side of the room towards the left side at a +45 degree angle. This includes the right half of the second pic. Imagine the ball spraying ink on the back side of the room during its trajectory.

edit: Actually this made me realize that the book had the ball thrown from the bottom left side of the room. I wish it had shown direction of ball in the diagram. My diagram is accurate if the ball has been thrown from the bottom right side of the room. So that solves the problem - the book did not properly show ball direction in a diagram that tackles the relativity of perception (an important time to be explicit about conditions).

 

[yuiop]

In every diagram, the ball is thrown from the bottom right side of the room towards the left side at a +45 degree angle. This includes the right half of the second pic. Imagine the ball spraying ink on the back side of the room during its trajectory.

edit: Actually this made me realize that the book had the ball thrown from the bottom left side of the room. I wish it had shown direction of ball in the diagram. My diagram is accurate if the ball has been thrown from the bottom right side of the room. So that solves the problem - the book did not properly show ball direction in a diagram that tackles the relativity of perception (an important time to be explicit about conditions).

I agree. If the book states the ball is going from right to left then the diagram is incorrect (it should look like your diagram).

 

[phyti]

DocZius;
I agree with you. The person in the room would accelerate with the ball, and not see any vertical movement, only horizontal motion.

 

[Daverz]

DocZius;
I agree with you. The person in the room would accelerate with the ball, and not see any vertical movement, only horizontal motion.

But the ball has an initial component of velocity in the vertical direction.