Question about Absolute Dependent Motion Analysis

[Oklid]

Homework Statement

[/B]

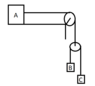
Find accelerations of these masses and the pulley are weightless.

Homework Equations

[/B]
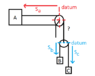
Sb+Sc=Length of the second rope (L2)

The Attempt at a Solution

[/B]

Just like I did, I placed all variables from datum to the masses.

In the second system, I write the equation as Sb+Sc=Length of the second rope (L2)

In the first, I couldn't write the equation with Sa, Sb, Sc. Because I couldn't define (?) with these Sb and Sc.

I could have done some mistakes, sorry.

 

[haruspex]

Because I couldn't define (?) with these Sb and Sc

So define a length for the first rope.
What you need next is to express the heights (or depths) of the two suspended masses in terms of these variables.

 

[Oklid]

So define a length for the first rope.
What you need next is to express the heights (or depths) of the two suspended masses in terms of these variables.

But I couldn't define a length with these variables Sc and Sb. Because they are a system their own. If there was a single block named as K instead of the second system and suspended to a with first rope. then first rope would be defined as Sa+Sc=L1.

 

[haruspex]

But I couldn't define a length with these variables Sc and Sb.

I am not suggesting you do.
L1 works fine as the length of the first rope. In terms of that and the variables you have, how far below the pulley are the two suspended masses?

 

[Oklid]

I am not suggesting you do.
L1 works fine as the length of the first rope. In terms of that and the variables you have, how far below the pulley are the two suspended masses?

I couldn't understand the question, sorry.

L1 works fine but again I can't define the L1 with these variables as Sa, Sb, Sc. When I define L1, It is L1 = Sa + (?).

But I solved it geometrically. I defined these accelerations aA, aB, aC.
Then I plused second system masses accelerations scalerly aB + aC. and as vectorial in the direction of -J.
With the help of Thales Theorem I found aA equal (aB+aC)/2.

Is this correct?

 

[haruspex]

L1 = Sa + (?).

Or more usefully ?=L1-Sa, so the depth of B below the top pulley is L1-Sa+Sb, etc.

aA equal (aB+aC)/2.

Yes,

 

[Oklid]

Or more usefully ?=L1-Sa, so the depth of B below the top pulley is L1-Sa+Sb, etc.

Yes, the depth of B below the top pulley is L1-Sa+Sb but with this, how can I do associate variables to get acceleration from lenghts?

 

[haruspex]

Yes, the depth of B below the top pulley is L1-Sa+Sb but with this, how can I do associate variables to get acceleration from lenghts?

Differentiate. Twice.

 

[Oklid]

Differentiate. Twice.

I didn't mention that, I know it.

I said when we know the depth of B below top datum, How I use it in my equations?

B has different datum point?

Edit: L2= Sc+Sb
L1= Sa+(?)
L1-Sa=(?)
Edit: I mean, yes we know that the depth of B below the top pulley is L1-Sa+Sb, so How can I use it?

 

[haruspex]

I didn't mention that, I know it.

I said when we know the depth of B below top datum, How I use it in my equations?

B has different datum point?

Edit: L2= Sc+Sb
L1= Sa+(?)
L1-Sa=(?)
Edit: I mean, yes we know that the depth of B below the top pulley is L1-Sa+Sb, so How can I use it?

I don't think I have grasped what your difficulty is.
Using y_α for depths below the top pulley, you have
$y_b=L_1-S_a+S_b$
$y_c=L_1-S_a+S_c$
$A_a=-\ddot{S_a}$
$A_b=\ddot{y_b}=\ddot{S_b}-\ddot{S_a}$
$A_c=\ddot{y_c}=\ddot{S_c}-\ddot{S_a}$
$S_b+S_c=L_2$
$\ddot{S_b}+\ddot{S_c}=0$
Hence $A_b+A_c=2A_a$, which you already found somehow.

Is your question where to go next? If so, you need to consider the tensions in the strings, the forces on the individual masses, and how these relate to their accelerations. You will not get more information out of the conservation of string lengths.

 

[Oklid]

I don't think I have grasped what your difficulty is.
Using y_α for depths below the top pulley, you have
$y_b=L_1-S_a+S_b$
$y_c=L_1-S_a+S_c$
$A_a=-\ddot{S_a}$
$A_b=\ddot{y_b}=\ddot{S_b}-\ddot{S_a}$
$A_c=\ddot{y_c}=\ddot{S_c}-\ddot{S_a}$
$S_b+S_c=L_2$
$\ddot{S_b}+\ddot{S_c}=0$
Hence $A_b+A_c=2A_a$, which you already found somehow.

Is your question where to go next? If so, you need to consider the tensions in the strings, the forces on the individual masses, and how these relate to their accelerations. You will not get more information out of the conservation of string lengths.

I think I know what my difficulty is.

When I wrote the equations, I decided the datums were unchangeable so the depth of masses below top pulley seemed unrelated to me.
I think I should seek more.

Thanks for helping, sir!

Edit: Spelling.