Question about driven coupled oscillator.

[ozone]

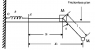
How does one go about plotting the effects of the frequency of the driving force vs the amplitude of the masses in a system such as the one pictured below?

Assume that I have already figured out what my two angular frequencies are, and the amplitues under driven force (the actually equations for the amplitudes are quite lengthy and I will try to refrain from writing it all out here)

The two frequencies for this system are$ω± = (1/2)(2ω^2p + ω^2s)±(1/2)\sqrt{ω^4p + w^4s}$

and I can plug these into our equations for the amplitude of my oscillators. However I find that there are some irreducible terms such as w^2p which are left behind.. I just can't seem to imagine how I am supposed to generate a graph Amplitude vs ω

 

[Simon Bridge]

The picture appears to show a mass on a spring with a pendulum coupled in.
It's like this one (unfortunately unfinished).

How is it being driven? By pushing the wall back and forth?
What is p and s? Your dimensions don't look like they match up - maybe I'm missing the context?

 

[ozone]

wp is the frequency of the pendulum and ws is the frequency of the spring.

 

[Simon Bridge]

<facepalm> subscript failure!
Here, let me:$$ω_\pm = \frac{1}{2}(2ω^2_p + ω^2_s) \pm \frac{1}{2}\sqrt{ω^4_p + w^4_s}$$
... OK, but you still have frequency on the LHS and frequency-squared on the right. Or did I miss something else and really need to get more sleep?

Are ω_p and ω_s the actual frequencies the components oscillate at or are they the natural frequencies without interference?

 

[Simon Bridge]

Oh wait! you are saying that since you don't have any values for some terms, you don't see how to plot amplitude vs frequency - since that would normally require actual numbers??
Is that right?

 

[ozone]

Well I am just saying that the plot is somewhat complex.. I notice that the key points where the shift in the graph occur are when ω is equal to exactly our ω_, our ω+, and our ωp terms.

However I don't know what to do in-between, and I am not sure how using just this and our equations for the amplitude of the block/pendulum we are supposed to generate a sufficient graph.

I can link you to the answer key for this problem set I was working on so that you can see for yourself.

Thanks.

 

[Simon Bridge]

Well I am just saying that the plot is somewhat complex.. I notice that the key points where the shift in the graph occur are when ω is equal to exactly our ω_, our ω+, and our ωp terms.

Hint: you can type a subscript with sub tags or in latex like this:

[noparse]
ω[sub]p[/sub], ω[sub]±[/sub]
[itex]\omega_p[/itex], [itex]\omega_\pm[/itex]
[/noparse]

Which renders as:
ω_p, ω_±
$\omega_p$, $\omega_\pm$

However I don't know what to do in-between, and I am not sure how using just this and our equations for the amplitude of the block/pendulum we are supposed to generate a sufficient graph.

What are the graphs supposed to demonstrate?

Normally I'd just invent some values and use a computer to generate the plots ... adjusting the values to bring out the features I want to show.