jaydnul
- 558
- 15
Euler gave us the below equations:
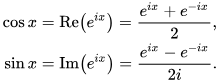
But this doesn't actually give me a number value for where the y value is when you plug in a number for x. For example, if i plug in 2pi for x, i know cosx should be 1. But that equation gives me (e^2i*pi +e^-2i*pi)/2. This doesn't give me 1. So what really is the point of the equation if you have to use the taylor series representation of sin and cos to interpret the results in the first place?
But this doesn't actually give me a number value for where the y value is when you plug in a number for x. For example, if i plug in 2pi for x, i know cosx should be 1. But that equation gives me (e^2i*pi +e^-2i*pi)/2. This doesn't give me 1. So what really is the point of the equation if you have to use the taylor series representation of sin and cos to interpret the results in the first place?