captainhampto
- 12
- 0
I have a general question about the Stern-Gerlach experiment. When a spin 1/2-particle passes through the magnets, is that effectively equivalent to applying a Hadamard transform to the state of the particle going through the apparatus?
Also, let's say I wanted to create a quantum circuit to reflect the Stern-Gerlach experiment. Would that basically be equivalent to:
H|q0> -> (measurement occurs) -> |q0> = |up> or |q0> = |down>
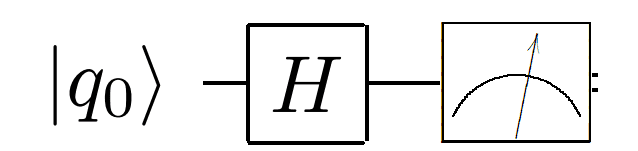
Also, let's say I wanted to create a quantum circuit to reflect the Stern-Gerlach experiment. Would that basically be equivalent to:
H|q0> -> (measurement occurs) -> |q0> = |up> or |q0> = |down>