Question About World Lines and Asymptotes

[gharkness]

I have a question regarding world lines and Minkowski diagrams. I have been looking everywhere for an answer and can't seem to find one, and I would just like some clarification.

So if we have a Minkowski Diagram, with a particular world line drawn out for, let's say a particle, is the world line required to respect the asymptotes that are in the plot on the line when ct/x = 1, or is the world line simply a path through space-time, where every single point on the line is an event?

If every single line is an event, would there be an individual set of asymptotes for each, with each event having its own hyperbola?

So, is the hyperbola only for an event, and any point falling on the hyperbola for that event can be achieved by a Lorentz Transformation?

Also, if what I thought about events was true, is it possible for different events on the same world line to be both space like and time like?

I have attached a picture with a world line doing what I am asking about, in case what I said was too hard to follow.

 

[PeterDonis]

I'm not sure I understand your questions, and rather than try to answer them as you ask them, I think it may be better just to state the standard definitions of the terms you're using:

An "event" is a point in spacetime. (Usually events are identified by something notable happening there: for example, "observers A and B passing each other" is an event.)

A "worldline" is a curve in spacetime; i.e., it is a 1-to-1 mapping of events to values of some parameter that labels points on the curve (where the parameter normally ranges from $- \infty$ to $\infty$). The term "worldline" is usually restricted to timelike curves (see below for the definition of "timelike"); such a curve must have a slope of greater than 45 degrees on a standard spacetime diagram (where time is vertical and space is horizontal), indicating that the object following the worldline is always moving slower than light (light rays travel on 45-degree lines in a spacetime diagram).

The terms "timelike", "null" (or "lightlike"), and "spacelike" can refer to two different types of things:

* They can refer to the relationship between a pair of events--this is usually phrased as the events being "timelike separated", "null separated", or "spacelike separated", and events which are spacelike separated can't be causally connected, whereas timelike or null separated events can be; or,

* They can refer to vectors, which can be thought of for our purposes here as little arrows that sit at some event (some point in spacetime) and point in a certain direction from that event. If the direction is more vertical than horizontal (i.e., slope greater than 45 degrees), the vector is timelike; if the direction is more horizontal than vertical (i.e., slope less than 45 degrees), the vector is spacelike; and if the slope is exactly 45 degrees, the vector is null.

Every curve in spacetime has a "tangent vector" at each event on it, which is just the vector that points in the direction of the slope of the curve at that event. So another way of describing a worldline (or "timelike curve") is that it's a curve whose tangent vector is timelike at every event on it.

Note that, as you can see from the above, individual events can't be spacelike, null, or timelike.

I'm not sure why you are asking about hyperbolas, but I can briefly describe how hyperbolas can come into play; there are basically two ways:

(1) Consider the set of all events which have a unit spacetime interval from the origin; i.e., events with coordinates $(t, x)$ such that $t^2 - x^2 = 1$ or $t^2 - x^2 = -1$. These sets of events form hyperbolas which asymptote to the lines you drew on your diagram (the dotted 45-degree lines that cross at the origin). The hyperbolas in the upper and lower "wedges" contain events which are timelike separated from the origin; the hyperbolas in the left and right "wedges" contain events which are spacelike separated from the origin. (Note that if we include the other two spatial dimensions, the timelike separated events form a hyperboloid of two sheets--to the future and past of the origin--while the spacelike separated events form a hyperboloid of one sheet.)

(2) Consider the worldline of an object that passes through the event $(t, x) = (0, 1)$ and has a constant proper acceleration (i.e., acceleration felt by the object itself) of $1$ in the positive $x$ direction. The worldline of this object will be the hyperbola $x^2 - t^2 = 1$, and it will, of course, asymptote to the two 45-degree lines you drew (it lies in the right "wedge" of the diagram). This worldline, and the family of hyperbolic worldlines that all asymptote to the same two 45-degree lines but pass through different $x$ coordinates at $t = 0$ (i.e., they all have worldlines of the form $x^2 - t^2 = x_0^2$), are very important in relativity physics.

After reading and digesting the above, you should hopefully be able to better formulate your questions (or perhaps the above will be sufficient to resolve them).

 

[ghwellsjr]

I have a question regarding world lines and Minkowski diagrams. I have been looking everywhere for an answer and can't seem to find one, and I would just like some clarification.

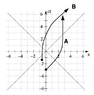
So if we have a Minkowski Diagram, with a particular world line drawn out for, let's say a particle, is the world line required to respect the asymptotes that are in the plot on the line when ct/x = 1,

If the particle is a photon or some other massless particle, then it must have a slope of plus or minus one although it can be anywhere on the diagram, it doesn't have to pass through the origin like the dashed lines in your drawing do. Otherwise, for all other particles that have mass, the slope can never be plus or minus one, like it appears the beginning of A and the ending of B do in your drawing, it has to be greater than one up to infinity or less then minus one up to minus infinity, like the remaining parts of your lines do.

or is the world line simply a path through space-time, where every single point on the line is an event?

That's true, too.

If every single [point on the] line is an event, would there be an individual set of asymptotes for each, with each event having its own hyperbola?

[I've added in what I think you meant to say, since that's the phrase you used in the previous sentence.]

You could say that every point (event) on the world line has a pair of asymptotes going out and up, one with a slope +1 and one with a slope of -1, which would represent visible photons that would propagate to other worldlines allowing all the particles to see each other, after some delay, of course.

There's no hyperbola in a single diagram representing a single Inertial Reference Frame (IRF) as you have made your diagram.

So, is the hyperbola only for an event, and any point falling on the hyperbola for that event can be achieved by a Lorentz Transformation?

Yes, if you sweep out a series of new diagrams derived by the Lorentz Transformation at different speeds and plotted the coordinates of an event, it would trace out a hyperbola.

Also, if what I thought about events was true, is it possible for different events on the same world line to be both space like and time like?

No, worldlines (for real particles with mass) can only be time like and every segment between any two events can only be time like. If you drew a line between two space like separated events, it would not be considered a legitimate world line because it would represent a particle traveling at faster than the speed of light which is not possible.

I have attached a picture with a world line doing what I am asking about, in case what I said was too hard to follow.

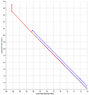
I have redrawn your diagram with some modifications. First, I added in dots along the world lines to represent 1-nanosecond increments of time for each particle. Second, I had both particles start at an earlier time so that the dots could be correctly placed. Third, I made the beginning of A and the ending of B be 99%c rather than 100%c which it looked like what you intended. (We can't have particles with mass traveling at the speed of light.) Fourth, I have added in some of those asymptotic photons propagating out and up at the speed of light going from one world line to the other one. (I am considering the speed of light to be 1 foot per nanosecond.) Here's the defining diagram:

I made this diagram by having the red particle stationary for 4 nsecs and then it traveled for 1 nsec at 0.2c, followed by 0.4c, 0.7c and finally 0.99c. The blue particle is the same pattern but in the opposite order. Note the dots that are connected by asymptotic light paths (I only drew in a few).

Now we transform to a speed of 0.2c which makes the segments that were traveling at 0.2c stationary. Note that the photons continue to propagate at 1c but connect the same pairs of events between the two particles:

Next we transform the original defining IRF to 0.4c:

​

Now 0.7c:

When we go to 0.99c, the drawing can get very large so I reduced the scale to half of what it was in the earlier diagrams:

But to make it easier to see the detail, I zoomed in on the upper left portion of the previous diagram:

Now that very long segment at the beginning of A and at the ending of B is just is just 1 nsec long and everything else is dilated.

Again, for all these diagrams, note that the thin lines representing the propagation of light between particular events on the two world lines conveys the same information in all the diagrams. This is why we can say that no IRF is preferred, they all contain exactly the same information.

Also, if you look at the top red event as you scan down through the IRF's, you can see how it traces out a hyperbola. The same is true for all the other events.

Well, I hope that I have answered your questions. If not, re-ask.