Solving the Flickering Light Paradox

[astrodummy]

TL;DR Summary

I refer to a project printed in Taylor and Wheeler's "Spacetime Physics" on pages 186-187. It was discussed here a while back but no satisfying solution was offered. I offer one here.

This post builds on a previously closed thread here:
https://www.physicsforums.com/threads/lightbulb-paradox.141191/#post-1145674

I will not describe the problem here without the copyright owner's permission. I, like the OP in the original thread, am keen to see if anyone else who has this text has solved the problem, since no solution is offered in the text.

My solution is to determine the spacetime interval between the power being disrupted to the bulb and the power being restored to the bulb in each reference frame. If these are the same then there is no paradox and special relativity holds.

NOTE: I mistakenly used 2 metres as the distance between the lamp and the start of gap instead of 4 meters in the rail frame and 1 meter instead of 2 in the slider frame. This does not affect the spacetime interval, just some of the event coordinates.

Event coordinates were determined used a spacetime diagrams (attached) drawn to scale and plotting the various world lines.

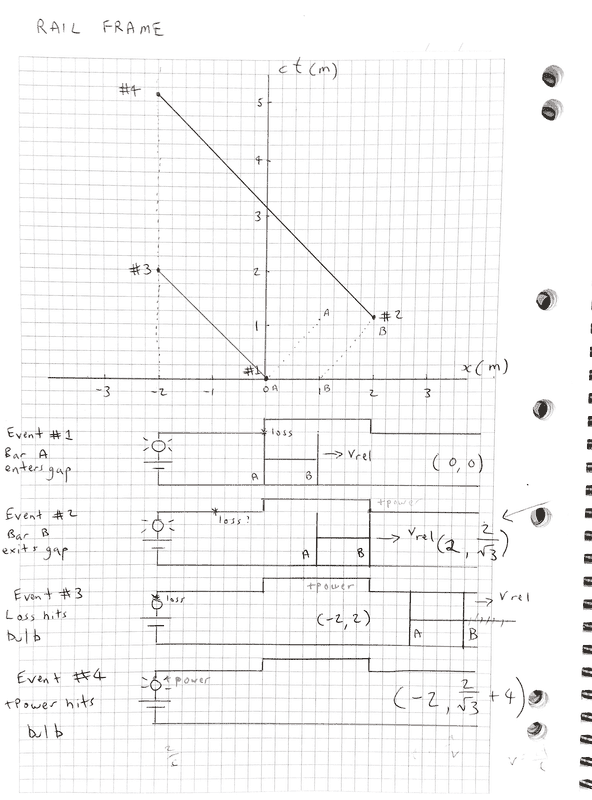
RAIL FRAME Event Coordinates
Working out the event coordinates in the rail frame is pretty easy. First plot the world lines of bar A and B on the slider as it traverses the gap in the top rail. The power lost world line starts as soon as the slider enters the gap and the power on world line starts when bar B reaches the end of the gap in the top rail. From there these world lines travel toward the left as light-like signals until they intersect with spatial line x=-2, where the bulb is. These intersections are easy enough to see on the spacetime diagram.

Event #1: Bar A enters gap
$(0,0)$

Event #2: Bar B exits gap
Time to travel 1 metre when $\gamma =2~is~\frac {2} {\sqrt{3}} m$
$(2,\frac {2} {\sqrt{3}} )$

Event #3: Power loss hits bulb
$(-2,2)$

Event #4: Power restored to bulb
$(-2,\frac {2}{\sqrt{3}}+4)$

So we are interested in the spacetime interval between Event #3 and Event #4.
This interval, as we know is given by $interval^2 = time^2 - space^2$ which is
$interval^2 = (\frac {2} {\sqrt{3}}+4 - 2)^2 - ( -2 - -2)$
$interval^2 = (\frac {2}{\sqrt{3}}+2)^2 - 0$
$interval = \frac {2} {\sqrt{3}}+2$ m

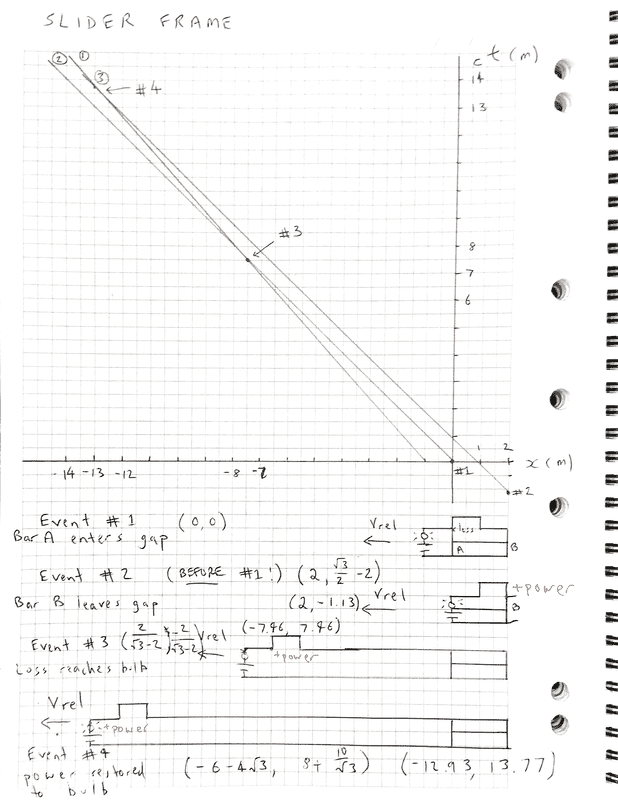
SLIDER FRAME Event Coordinates
Things get a little more involved in the slider frame since both the rail and the power off and on signals travel to the left relative to the at rest slider. I had to derive the linear equations for the power off and power on world lines, then determine the intersections with the bulb world line in order to arrive at the event coordinates #3 and #4.

Linear equations

Bulb worldline
$ct=-\frac{2}{\sqrt{3}}(x+1)~~~$[1]
Power off worldline
$ct=-x~~~$[2]
Power on worldline
$ct=-x-\frac{2}{\sqrt{3}}+2~~~$ [3]

Find intersection of line [1] and [2] to derive Event #3 coordinates
$-x = - \frac {2}{\sqrt{3}}(x+1)$
$x= \frac {2}{\sqrt{3}-2}$
$ct=\frac {-2}{\sqrt{3}-2}$

Find intersection of line [1] and [3] to derive Event #4 coordinates
$-x+\frac {\sqrt{3}} {2} = \frac {-2} {\sqrt{3}}(x+1)$
$x = -6 - 4\sqrt{3}$
$ct = 8 + \frac {10} {\sqrt{3}}$

Event #1: Bar A enters gap
$(0,0)$

Event #2: Bar B exits gap ( BEFORE Event #1! )
$(2,\frac {\sqrt{3}} {2})$

Event #3: Power loss hits bulb
$(\frac {2} {\sqrt{3}-2},\frac {-2}{\sqrt{3}-2})$

Event #4: Power restored to bulb
$(-6-4 \sqrt{3},8+\frac {10}{\sqrt{3}})$

Now at last we can determine the spacetime interval between Event #3 and Event #4.
This interval, as we know is given by $interval^2 = time^2 - space^2$ which is
$interval^2 = (8+\frac{10}{\sqrt{3}}+\frac {2}{\sqrt{3}-2})^2 - (-6 -4\sqrt{3} - \frac {2} {\sqrt{3}-2})^2$
$interval^2 = (4+\frac{4}{\sqrt{3}})^2 - (-2(1+\sqrt{3}))^2$
$interval^2 = \frac{32}{3}(2+\sqrt{3}) - 8(2+\sqrt{3})$
$interval^2 = \frac{8}{3}(2+\sqrt{3})$
$interval = \frac{2}{\sqrt{3}}+2$ m

CONCLUSION
Since the spacetime interval between Events #3 and #4, the bulb flickering off and back on, is the same in each reference frame there is no paradox. Special Relativity still works!

 

[astrodummy]

Oops ... found an error on the line after:
"Find intersection of line [1] and [3] to derive Event #4 coordinates"

Next line SHOULD BE:

$-x-\frac{2} {\sqrt{3}}+2 = -\frac{2} {\sqrt{3}}(x+1)$

which simplifies to

$x = -6 - 4\sqrt{3}$

same as before.

 

[pervect]

I don't see how you expect us to comment without a description of the problem being analyzed. I don't recall the "fair use" provisions of the copyright law, unfortunately - which may be US centric in any case.

 

[Ibix]

I don't see how you expect us to comment without a description of the problem being analyzed. I don't recall the "fair use" provisions of the copyright law, unfortunately - which may be US centric in any case.

Taylor and Wheeler recently made their book free to download: http://www.eftaylor.com/spacetimephysics/.

Edit: The example is near the end of chapter 6.

Edit 2: The book was released under a Creative Commons license that specifically permits copying and remixing as long as it is properly attributed.

 

[Ibix]

A couple of comments.

First, you derived the coordinates of the events in the slider frame from physical reasoning in that frame. You can sanity check it by Lorentz transforming the events in the rail frame. For example, event #3 is at $(x,t)=(-2,2)$, which transforms to the slider frame as $$\begin{eqnarray*}
(x',t')&=&\left(2(-2-\frac {\sqrt{3}}22),2(2+\frac {\sqrt{3}}22)\right)\\
&=&(-4-2\sqrt{3},4+2\sqrt{3})
\end{eqnarray*}$$Checking that this is the same as your expression and checking event 4 are left as exercises for the reader.

Second, you seem to have assumed that the signal speed in the wires is $c$. It probably isn't, so you should probably consider whether a slower signal speed makes any difference (unless the exercise says to assume that somewhere and I've missed it). No maths needed, but a line or two of reasoning why it doesn't matter.

Finally, I would say that to truly show that there is no paradox you would have to show that the current via the right-hand bar doesn't reach the left-hand end of the offset until after the left-hand bar has disconnected. Incidentally, you've mislabelled the bars as A and B. In the book, A and B are points on the rails, and the bars are labelled C and D.

 

[astrodummy]

Ibix,

Thanks for your feedback. I should have known to double-check the coordinates by doing a Lorentz transformation. My coordinates are okay since I mistakenly used 2 metres as the distance between the bulb and point A in the rail frame, instead of 4 metres. And I mislabeled my diagram. D'oh.

Interesting about your point regarding the speed of electricity being less than c. Intuitively if should make no difference to the answer, unless this speed is slow that the speed of the slider relative to the rail. The worldlines of the 'power off' and 'power on' signals will simply have a more timelike vector.

Good to see my solution wasn't completely crazy!

Steve

 

[astrodummy]

Taylor and Wheeler recently made their book free to download: http://www.eftaylor.com/spacetimephysics/.

Edit: The example is near the end of chapter 6.

Edit 2: The book was released under a Creative Commons license that specifically permits copying and remixing as long as it is properly attributed.

Thanks Ibix,

For the lazy I have attached some screenshots.

Steve

 

[astrodummy]

Ibix,

...
My coordinates are okay since I mistakenly used 2 metres as the distance between the bulb and point A in the rail frame, instead of 4 metres.
...

Steve

No no no, my bad. $(-4-2\sqrt{3},4+2\sqrt{3})$ equals $(\frac{2}{\sqrt{3}-2},\frac{-2}{\sqrt{3}-2})$

In my defense I'm nearly 60 yo and haven't done this kinda maths for a couple of years.

Steve

 

[anuttarasammyak]

I am very much interested in this "paradox". Thank you @astrodummy.

Say the relative speed v_rel << c, small compared with c, we find the loss of contact on left edge and gain of contact on right edge of Slider are simultaneous events both in Rail frame and in Slider frame because we do not have to be sensitive on the difference of simultaneity of frames for such a low speed.

In this case Light bulb flickers. Signal : loss of contact and signal : gain of contact take place simultaneously but left edge is nearer to light bulb than right edge by 2 meter=l. Time difference for signals to reach light bulb is $\frac{l}{c}=7.77$ nano second. Light bulb is turned off during 7.77 nano second.

So I assume light bulb flickers in both the frames for original $v_{rel}=\frac{\sqrt{3}}{2}c$ case. It is obvious for Rail frame. In Slider frame also I assume loss of contact signal arrives to light bulb earlier than gain of contact signal though gain of contact takes place earlier than loss of contact in Slider frame, considering that light bulb is evacuating with speed $v_{rel}=\frac{\sqrt{3}}{2}c$ from light speed c signals. Gain of contact signal arrives at right edge rail in the middle way to light bulb, after loss of contact signal has departed from there. Your opinion is appreciated.

EDIT miscalculation False 7.77 True 6.67 nano second. Thanks @astrodummy #12.

 

[astrodummy]

If v_rel << c then $\gamma$ will be 1. So, no length contraction in either reference frame. And since AB = CD the bars will always be in contact with the rails, so the power will never be lost to the bulb. No flicker at all!

As Ibix correctly pointed out the quickest way to determine the event coordinates in the slider frame is to do a lorentz transformation on the rail frame coordinates $(-2,2)$ and $(-2, \frac{2}{\sqrt{3}}+4)$ which yeilds $(-4-2\sqrt{3},4+2\sqrt{3})$ and $(-6-4\sqrt{3},8+\frac{10}{\sqrt{3}})$.

The spacetime interval between the bulb going off and back on again is $\frac{2}{\sqrt{3}}+2$ metres in both frames of reference.

 

[anuttarasammyak]

I say flicker, you say no. Please have a look at attached 4 sketches on time evolution for the post #9, v_rel << c case to explain flicker. Power on/off signal has light speed.

 

[astrodummy]

D'oh! Of course. That 2m section of the rail is "dead" the instant Bar D touches point B. So that 2 meters of 'no power' will get to bulb in due course. So coordinates of Event #3 'power loss reaches bulb' is $(-4,4)$ and coordinates of Event #4 'power restore reached bulb' is $(-4,6)$. So the spacetime difference is 2 m as you would expect or 6.67 nanoseconds. And since $\gamma$ = 1 the slider frame behaves in the identical fashion.

 

[anuttarasammyak]

I draw similar time evolution 4 rough sketches in Silider frame for $v_{rel}=\frac{\sqrt{3}}{2}c$ to explain flicker as attached. I should appreciate if you could provide certificate by calculation.

 

[astrodummy]

D'oh! Of course. That 2m section of the rail is "dead" the instant Bar D touches point B. So that 2 meters of 'no power' will get to bulb in due course. So coordinates of Event #3 'power loss reaches bulb' is $(-4,4)$ and coordinates of Event #4 'power restore reached bulb' is $(-4,6)$. So the spacetime difference is 2 m as you would expect or 6.67 nanoseconds. And since $\gamma$ = 1 the slider frame behaves in the identical fashion.

Your 'time evolution' diagrams have a problem. You cannot claim that AB is in 'black out' before bar D gets to B without also acknowledging that the bottom rail between C and D ( the distance between the vertical bars on the slider ) is ALSO in 'black out'. Since there can be no current in either the instant before D makes contact with B. So the 'dead time' should be 4 m ( length of slider plus length of the gap ) perhaps?

 

[astrodummy]

Your 'time evolution' diagrams have a problem. You cannot claim that AB is in 'black out' before bar D gets to B without also acknowledging that the bottom rail between C and D ( the distance between the vertical bars on the slider ) is ALSO in 'black out'. Since there can be no current in either the instant before D makes contact with B. So the 'dead time' should be 4 m ( length of slider plus length of the gap ) perhaps?

Actually now that I think about it that cannot be true either. Both the top and bottom rails are always 'live' since they are both connected to the battery at all times. Instantaneously changing the connection from bar A to bar B will not interrupt the current flow when vrel << c. There will be no flicker.

 

[PeterDonis]

Both the top and bottom rails are always 'live' since they are both connected to the battery at all times.

This is wrong. The battery can only discharge in one direction.

There will be no flicker.

You are incorrect.

The facts of the scenario that guarantee that there will be a flicker are:

(1) The rest length of the moving bar is the same as the rest length of the gap between A and B.

(2) The moving bar is moving, relative to the rail, in the direction away from the bulb.

(3) The current that lights the bulb travels at the speed of light. (In an actual wire it would be slower, but using $c$ as the speed is easier for a thought experiment as it makes the speed frame invariant.)

These three facts imply the following in the rest frame of the rail:

(RA) An instant before the moving bar disconnects from the rail at point A, the other end of the bar has not quite reached point B, so the other end is disconnected from the rail and has been for however long it takes the bar to cover the gap from A to B. That means that at this instant, the only way a circuit can be completed is to flow through point A. (In the limit of zero velocity, the bar can just be touching points A and B--so any velocity at all shortens the bar by some amount and ensures that the bar must disconnect from A before it connects to B.)

(RB) Once the bar disconnects from the rail at point A, no current is flowing from point A--since the bar has disconnected there and no current can be coming (yet) from point B because of the finite speed of the current.

(RC) Therefore, there will be a gap in the current for however long it takes for current to flow from point B to point A, and this gap in current will cause the bulb to go off and then on again when the gap ends--i.e., to flicker.

The three facts (1), (2), (3) also imply the following in the rest frame of the bar:

(BA) At the instant the rail connects to the bar at point B, the rail is still connected at point A. Therefore, at the instant the rail disconnects from the bar at point A, it is already connected at point B.

(BB) However, the time between the rail connecting at point B, and disconnecting at point A, is less than the time it takes light to travel the length of the bar (since in this frame, that is the spatial distance from the "connect" point to the "disconnect" point).

(BC) Therefore, there will be a gap in the current for a time equal to the difference between those two times (light travel time from B to A, minus time between rail connect at B and disconnect at A).

Drawing a spacetime diagram can help to visualize the above.

 

[astrodummy]

So in this scenario only the bottom rail in considered 'live' along it's entire length and as the slider bar C breaks contact at A and bar D touches contact B immediately afterwards there will be a 2m delay in the supply to current to the bulb which it will 'see' in 4m time. Assuming electricity speed = c, which is it isn't, but the flicker will be 2m regardless.

 

[PeterDonis]

Assuming electricity speed = c, which is it isn't

True, but assuming a slower speed just complicates the math (because now we can't assume that the speed of the current is frame invariant--we have to transform it when we transform between frames) without changing the essential result (because the velocity transformation law ends up leading to the same conclusion, just with more complicated math).

the flicker will be 2m regardless

No, it won't. It will be longer if the speed of the current is slower. Also, the length of time of the flicker is not the same in both frames. (The spacetime interval between the "current off at bulb" and "current on at bulb" events is frame invariant, as all intervals are, but it is only the same as the "length of time of the flicker" in the rail frame, since that is the bulb's rest frame.)

 

[anuttarasammyak]

So the 'dead time' should be 4 m ( length of slider plus length of the gap ) perhaps?

Though I am not sure I catch you, rather complex energy flow even in the case of such a simple circuit, explained in http://amasci.com/elect/poynt/poynt.html as an example, might be helpful ( or bring more troubles ?) to share a right picture.

 

[astrodummy]

True, but assuming a slower speed just complicates the math (because now we can't assume that the speed of the current is frame invariant--we have to transform it when we transform between frames) without changing the essential result (because the velocity transformation law ends up leading to the same conclusion, just with more complicated math).
No, it won't. It will be longer if the speed of the current is slower. Also, the length of time of the flicker is not the same in both frames. (The spacetime interval between the "current off at bulb" and "current on at bulb" events is frame invariant, as all intervals are, but it is only the same as the "length of time of the flicker" in the rail frame, since that is the bulb's rest frame.)

You're right, the gradient of the 'current off' and 'current on' world lines will be more timelike so when they intersect with the vertical bulb world line they will have a wider separation.

 

[astrodummy]

I draw similar time evolution 4 rough sketches in Silider frame for $v_{rel}=\frac{\sqrt{3}}{2}c$ to explain flicker as attached. I should appreciate if you could provide certificate by calculation.
View attachment 276074View attachment 276075View attachment 276076View attachment 276077

In the slider reference frame you still have the 2m flicker PLUS the time it takes for the slider to clear the 1m gap. At vrel = $\frac{\sqrt{3}}{2}$ it takes $\frac{2}{\sqrt{3}}~m$ of time to clear the gap. So the total flicker time is now $\frac{2}{\sqrt{3}}+2~m$, the same as in the rail frame.