Question on basic circuit analysis

[dect117]

Homework Statement

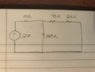
See attachment "image2"

Relevant Equations

V=IR

My initial attempt had me combining the 40 and 20 ohm resistors in series, then combining the result with the 120 ohm resistor in parallel (top).

However, this was incorrect. According to my answering guide, the correct method was to transform the voltage source into a current source, then combine the 10 and 120 ohm resistors in parallel. Finally, you're supposed to add the 60 ohm equivalent resistor at the end after reverting the current source back to a voltage source (bottom), which would end up dropping by 1 volt.

This seems confusing and counter to every other circuit I've analyzed this semester. Can someone explain to me what's going on here?

 

[NascentOxygen]

Your steps in image 1 are all correct. But what exactly are you being asked to determine—what is the problem statement in words?

 

[FactChecker]

You seem to be talking about two different problems and diagrams. I don't see how they can be related.

And I don't agree with the calculations in the bottom row of image1. All three resisters are in parallel and are equivalent to a single 8-ohm resistor.

 

[dect117]

Your steps in image 1 are all correct. But what exactly are you being asked to determine—what is the problem statement in words?

You seem to be talking about two different problems and diagrams. I don't see how they can be related.

And I don't agree with the calculations in the bottom row of image1. All three resisters are in parallel and are equivalent to a single 8-ohm resistor.

Technically, I'm supposed to solve an RL circuit. I went ahead and drew the circuit with the inductor and switch (image3). Currently, I'm stuck on the first part: find the currents I_L, I_O, and the voltage across the inductor at t=0. However, at t=0, the inductor shorts and the wire with the switch effectively isn't there since the switch is open, hence my drawing in image2.

The answers I got for I_L, I_O, and V_L are 160mA, 0A, and 0V, respectively. Those are the correct answers.

I got 160mA for I_Lby using voltage divider, which gave me the voltage across the 10 ohm resistor, 2.4V, and the current being supplied to the circuit, 240mA. Using KCL, I got the following equations:
$$i=i_1 + i_2$$
$$12=10i + 120i_1$$
$$120i_1=60i_2$$
$$60i_2=12-10(.24)$$
$$i_2=I_L=\frac {9.6} {60}=.16$$
Technically using the bottom method in image1 works, but it doesn't seem right to me. I'm also worried that if I don't use the right method, even if I get the correct answer I'll get points docked on my next test.

 

[NascentOxygen]

So you are required to find the current through the 60Ω resistor. This will not be equal to the current through the 50Ω resistance, but it will be a proportion of it. The current in the 50Ω represents the current drawn from the battery, and comprises that in the 60Ω plus that in the 120Ω.