Calculating Current in a Series RC Circuit

[IronaSona]

Hi , i was just wondering how would i find the current through a capacitor (Series RC circuit)

I found a questions online which asks to find the voltage and the current through a capacitor at 1kHz and 10Khz

Capacitor = 0.01uF
Resistor = 100 Ohms
Voltage Source = 10v

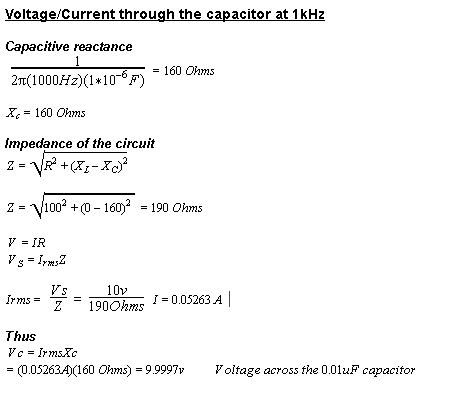
ive done some calculations but not sure they are 100% correct too

 

[BvU]

0.01 $\mu$F is $10^{-8}$ F

$\$

 

[IronaSona]

0.01 $\mu$F is $10^{-8}$ F

$\$

so would it be 0.00062A across the capacitor ?

 

[BvU]

I found a questions online which asks to find the voltage and the current through a capacitor at 1kHz and 10Khz

So my advice is: treat it as homework

• Provide a complete problem statement ( Now we have to reconstruct this is about a RC series circuit -- from something you are not sure about )
• list the relevant equations
• clarify what the symbols used stand for

I'm not all that happy with the didactics of the treatment here but others may disagree.

You have

With (a bit much, but elementary): $$\begin{align*} V_0 &= |V_0| e^{j\omega t} \\ V_0 &= Z_{\text tot} I \\ Z_{\text tot} & = Z_R + Z_C \\V_C &= V_0 {Z_C\over Z_{\text tot}} \\
Z_R &= R\\Z_C &= {1\over j\omega C} \\V_C &= Z_C I\end{align*}$$
easy to solve, no reason for uncertainty.

However, I have assumed you are familiar with complex numbers - something I have to guess because it's not evident from your original post.

If you are not, I recommend picking it up:

I recall a short writeup by @LCKurtz title There’s nothing imaginary about complex numbers. It's more for teachers but there are similarities with Smith (like in Kurtz 3.1). It sure has the advantage of being al lot more concise !
Lynn's other writeup alternating current impedance is also quite good in your context.

(Smith is "The Scientist and Engineer's Guide to Digital Signal Processing")

$\$

 

[boo]

This is a sinusoidal steady state problem. For some reason you have calculated only the magnitude of the voltage and current and not the phase. Also, as others have mentioned 0.01uF = 10^-8 F. Not sure what is expected of you but since this is a series circuit just divide the voltage by the complex impedance which (at 1k Hz) in this case is just 100 - j * (1/(2*pi*10^3*10^-8)). That would be the current. The voltage would then be the current * (- j * (1/(2*pi*10^3*10^-8)). If you are just interested in magnitudes then of course take the square root of the sum of the square of the impedances and do the same thing.