Question on trajectory of a particle attached to a string on a inclined plane

[rkrthegreat]

Homework Statement

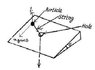
A particle is placed on a rough plane inclined at an angle theta, where tan θ = μ = coefficient of friction(both static an dynamic). A string attached to the particle passes through a small hole in the plane. The string is pulled so slowly that you may consider the particle to be in static equilibrium at all times. Find the path of the particle on the inclined plane.

Homework Equations

In equilibrium, by lami's theorem, A/sina = B/sinb = C/sinC

The Attempt at a Solution

I have applied lami's theorem, taking three concurrent forces as mgsintheta, friction f and tension T, but am not getting any idea how to proceed to find the trajectory.

 

[rl.bhat]

To get the equilibrium condition, tension and frictional force must be perpendicular to each other. It is possible when the particle moves like a pendulum with reduced length and constant speed.

 

[rkrthegreat]

I don't get it sir, why should the Tension and friction be perpendicular to each other? It would be very helpful if you could give a more elaborate explanation of this, and how you approached the problem.

 

[rkrthegreat]

Here's the diagram given in the book (problems in physics by Abhay Kumar Singh) for further clarification of the situation:
http://www.goiit.com/posts/downloadAttach/35730.htm

 

[rl.bhat]

The motion of the particle is perpendicular to the tension.
The frictional force is always in the apposite direction of the motion. Hence fr is perpendicular to the tension. As the particle moves down, First tension decreases and then increases. whereas the frictional force first increases and then decreases. Now you can decide, what should be the trajectory.

 

[rkrthegreat]

One last clarification required sir, could you also explain why the particle moves perpendicular to the tension?

 

[rl.bhat]

One last clarification required sir, could you also explain why the particle moves perpendicular to the tension?

In this problem the particle moves due to two forces. One due to the component of mg, which is perpendicular to the string. Another due to the slow pull to the string, which is along the string, towards the hole. So there are two frictional forces.

 

[rkrthegreat]

The motion of the particle is perpendicular to the tension.
The frictional force is always in the apposite direction of the motion. Hence fr is perpendicular to the tension. As the particle moves down, First tension decreases and then increases. whereas the frictional force first increases and then decreases. Now you can decide, what should be the trajectory.

But won't the particle move along the direction of the string also? Since it is being pulled, length of the string is decreasing with time, so the particle should have one component of its motion along the string too.
I have attached a diagram as to how the forces are directed in my opinion. The three forces (friction f = μmg cosθ = mg sinθ, component of mg down the plane = mg sinθ, and tension in the string T) should be aligned at all times such that the particle remains in equilibrium, so how can the particle move always perpendicular to the tension? I am not able to understand this.

 

[rkrthegreat]

A little more detailed, step by step reply in one post would be very good, sir, because this is my first encounter with these types of problems. You see, I am in class 11th, in India, preparing for IIT JEE, and I am very much interested in physics, so this question is not exactly a homework or coursework question, I have taken it up after solving problem books like IE Irodov, but I can not seem to find a way to solve this very problem. I know the rules of this forum that direct solutions should not be given, and I am not asking for one, but this problem is obviously not one of the regular ones in school classrooms, so I need some more detail in the answers so that I can grasp the solution properly. None of my schoolteachers have been able to solve it yet, and I don't know where to get the method of solving this problem. So I posted it on this forum, and sir, with your huge experience and vast knowledge, I think you can certainly help me get over this problem. I am looking forward to your reply sir, hoping I can solve this problem then.

 

[rl.bhat]

In the post #7, I have taken into account two motions of the particle. One due to the component of mgsinθ, and the second due to the second component of mgsinθ and pull.
When you say the particle remains in equilibrium, do you mean that three angles between the three forces remain same in spite of the motion of the particle?