nyguy
- 2
- 0
I humbly ask if someone can please help me dissect this problem. The problem is worded verbatim and I explained how I initially approached it. Please help.
Two crickets, Chirpy and Milada, jump from the top of a vertical cliff. Chirpy jumps horizontally and reaches the ground in 3.50s. Milada jumps with an initial velocity of 95.0 cm/s at an angle of 32.0 degrees above the horizontal. How far from the base of the cliff will Milada hit the ground.
The equations below SHOULD meet the requirements to finding the answer to this problem.
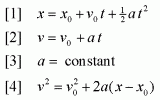
Initially when I approached this problem, it made sense to find the height of the cliff. So, I took the first cricket's time (Chirpy) which was 3.50s and used it to find the height. I used Equation 1. The height that I came up with was 60.025m. In most cases, if not all, the units when dealing with velocity and acceleration problems are usually in meters per second. So, I converted the velocity vector to meters/second and then attempted at finding its corresponding components. After the conversion, 95.0 cm/s is equivalent to .95 m/s. Since this problem is in 2-dimension, I just had to find Vx and Vy, the components of the velocity vector.
The components are as follows:
Vx=(Cos 32) x .95 = .806 m/s
Vy= (Sin 32) x .95 = .503 m/s
Assuming that I'm making the right decision, I made an attempt at finding the second cricket's (Milada) max height when it jumped off of the cliff at a 32 degree angle above the horizontal. I used Equation 4. I have an understanding that when a particle, projectile, or living thing reaches a max height in the air, the velocity is zero due to the constant acceleration pushing down on it. So, I set equation 4 to zero.
These were my calculations:
0=-(.503)^2 + 2(-9.8)(y)
y=.013m
The last thing I did before I was lost was added the max height onto the cliff's height which was 60.038m. I didn't have a clue as to what to do next. How do I find how far from the base of the cliff the second cricket will land?? Do I need to find a new time, a new velocity since the cricket is now in free fall, what?? Please help.
Homework Statement
Two crickets, Chirpy and Milada, jump from the top of a vertical cliff. Chirpy jumps horizontally and reaches the ground in 3.50s. Milada jumps with an initial velocity of 95.0 cm/s at an angle of 32.0 degrees above the horizontal. How far from the base of the cliff will Milada hit the ground.
Homework Equations
The equations below SHOULD meet the requirements to finding the answer to this problem.
The Attempt at a Solution
Initially when I approached this problem, it made sense to find the height of the cliff. So, I took the first cricket's time (Chirpy) which was 3.50s and used it to find the height. I used Equation 1. The height that I came up with was 60.025m. In most cases, if not all, the units when dealing with velocity and acceleration problems are usually in meters per second. So, I converted the velocity vector to meters/second and then attempted at finding its corresponding components. After the conversion, 95.0 cm/s is equivalent to .95 m/s. Since this problem is in 2-dimension, I just had to find Vx and Vy, the components of the velocity vector.
The components are as follows:
Vx=(Cos 32) x .95 = .806 m/s
Vy= (Sin 32) x .95 = .503 m/s
Assuming that I'm making the right decision, I made an attempt at finding the second cricket's (Milada) max height when it jumped off of the cliff at a 32 degree angle above the horizontal. I used Equation 4. I have an understanding that when a particle, projectile, or living thing reaches a max height in the air, the velocity is zero due to the constant acceleration pushing down on it. So, I set equation 4 to zero.
These were my calculations:
0=-(.503)^2 + 2(-9.8)(y)
y=.013m
The last thing I did before I was lost was added the max height onto the cliff's height which was 60.038m. I didn't have a clue as to what to do next. How do I find how far from the base of the cliff the second cricket will land?? Do I need to find a new time, a new velocity since the cricket is now in free fall, what?? Please help.