Question regarding Rolling with and without Slipping and Sliding

[Harikesh_33]

Homework Statement

So these are few questions my prof has asked us to try answering :

Examine through the lens of Frictional forces and rolling with and without Slipping and Sliding as to

1)what happens when a car wheel is stuck in a mud and finds it hard to get out of the mud .

2)what happens to a wheel in an incline .

3)what happens to a wheel when it's rolling without Slipping

Relevant Equations

1)$v_{cm}$=$Rω$ (rolling without Slipping).
2)$v_{cm}$>$Rω$ (rolling with sliding) .
3)$v_{cm}$<$Rω$ (rolling with slipping) .
4)$τ_{friction}$=$R×F_f$(F_f ca be either kinetic or static friction based on the situation)

1)When a wheel is stuck in mud it rolls with slipping ,this means that at the point of contact it has a net velocity

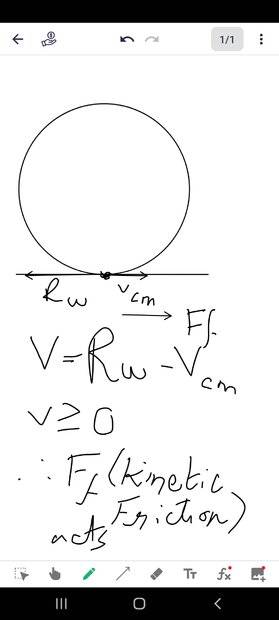
As we can see from the image Kinetic Friction acts in the direction opposite to the resultant velocity ,this effectively reduces the tangential velocity at the surface and tries to brings it to Rolling without Slipping condition.Now can you tell me what happens after that ?Does the wheel get out of the mud ? I know that once the relative velocity betweent the wheel and surface becomes zero.Static friction sets in ,do I have to achieve Rolling with Sliding to get out of the mud ?


2)

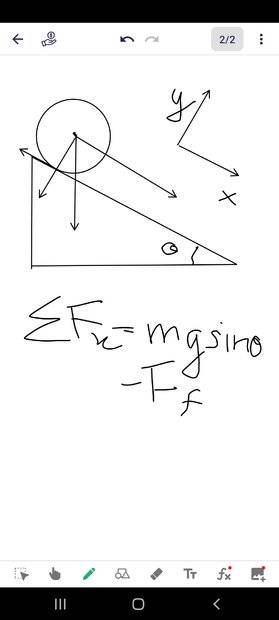If I am not mistaken the job of Static Friction is to make sure that the Rolling without Slipping or sliding is maintained .Now if the net force is non zero then it means that there is an acceleration of Centre of mass ,Now there is a Torque due to Static Friction ,this causes an angular acceleration α ,this leads to an acceleration of its own ,now the condition for rolling without Slipping /Sliding is that $a_{cm}=Rα$ (where $a_{cm}$ is the acceleration due to Force in x direction ,α is the acceleration due to the angular acceleration ,when $a_{cm}>Rα$ then Rolling with Sliding happens .

3)When a wheel is Rolling without Slipping the relative velocity is zero ,which mean Static friction exists ,now for the wheel to move in Rolling with Slipping or Sliding the acceleration produced due to the angular acceleration caused by the Torque, should be less than acceleration of the Centre of Mass .

I would love to hear your thoughts on my answer .

 

[Lnewqban]

Regarding #1:
The wheel must have constant torque applied in order to rotate on the mud.
More than a point of contact, there is a portion of the tire's surface that is surrounded by mud, some of which sticks to it and is removed from or pumped out the area of contact.
Because of that, the wheel digs into the mud and its center of mass gets lower and lower.

While all that happens, only kinetic friction is present.
I see no reason for the relative velocities to tend to zero, as you explain.
Even if they do, because the wheel's surface finally finds areas of mud having better coeficient of friction, it now needs higher friction force to climb out of the formed cavity and move the center of mass upwards.

I believe the example is not as good as the one of a wheel slipping on a hard surface of poor coefficient of friction.

 

[Harikesh_33]

Regarding #1:
The wheel must have constant torque applied in order to rotate on the mud.
More than a point of contact, there is a portion of the tire's surface that is surrounded by mud, some of which sticks to it and is removed from or pumped out the area of contact.
Because of that, the wheel digs into the mud and its center of mass gets lower and lower.

While all that happens, only kinetic friction is present.
I see no reason for the relative velocities to tend to zero, as you explain.
Even if they do, because the wheel's surface finally finds areas of mud having better coeficient of friction, it now needs higher friction force to climb out of the formed cavity and move the center of mass upwards.

I believe the example is not as good as the one of a wheel slipping on a hard surface of poor coefficient of friction.

Correct me if I am wrong ,but the constant Torque is provided by the Kinetic Friction here .

Doesn't a lower centre of mass make it even harder to get out of the mud ? (Lower Centre of Mass -an object becomes more stable ) .

Isn't the job of Kinetic Friction to attain Rolling without Slipping ?

 

[Lnewqban]

Correct me if I am wrong ,but the constant Torque is provided by the Kinetic Friction here .

Doesn't a lower centre of mass make it even harder to get out of the mud ? (Lower Centre of Mass -an object becomes more stable ) .

Isn't the job of Kinetic Friction to attain Rolling without Slipping ?

The constant torque is provided by the shaft of the wheel; without it, neither rotation nor kinetic friction would happen.
Kinetic friction induces a constant torque that resists rotation (it tries to stop the wheel from spinning, without achieving it in this case).

It is easier for a car to roll over a short obstacle than to roll over a tall one.

For two flat surfaces in contact (imagine a wheel huge diameter), we know that there is kinetic friction when one slides respect to the other.
We also know that the magnitude of that frictional force is always smaller than the magnitude of maximum force induced when the surfaces keep from sliding (static friction).

When we are pushing a heavy piece of furniture, it is harder to make it slide than to keep sliding it.
Once sliding (kinetic friction), it never returns to static by itself; therefore, once spinning (kinetic friction) without rolling, the wheel can't roll (static friction) without sliding by itself, unless conditions change.

 

[Lnewqban]