mazia
- 28
- 2
- Homework Statement
- The Pearson question is:
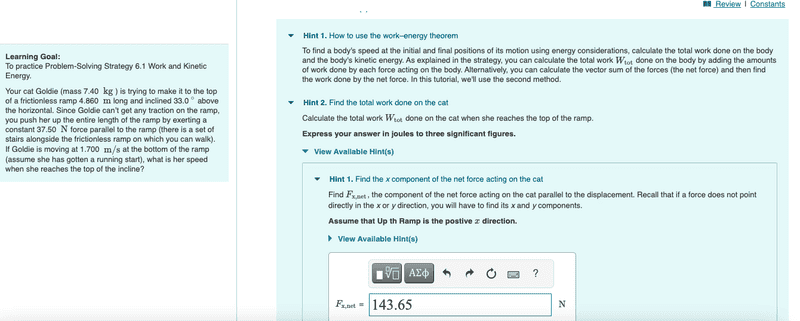
Your cat Goldie (mass 7.40kg) is trying to make it to the top of a frictionless ramp 4.860m long and inclined 33.0∘ above the horizontal. Since Goldie can’t get any traction on the ramp, you push her up the entire length of the ramp by exerting a constant 37.50N force parallel to the ramp (there is a set of stairs alongside the frictionless ramp on which you can walk). If Goldie is moving at 1.700 m/s at the bottom of the ramp (assume she has gotten a running start), what is her speed when she reaches the top of the incline?
- Relevant Equations
- First tried using
F-mg*sin(theta)=ma to solve for a, then using vf^2=vo^2+2as, but then I realized I didn't know what the displacement was.
Then, since I'm asked to find Fnet, I tried
Fn = mg*cos(theta) -> (72.59N)cos(33.0) = 60.88N
Fnet = Fg+Fn+Fapplied -> (72.59N)+(60.88N)+(37.5N) = 171.28N
Fx,net = Fnet*cos(theta) -> 171.28*cos(33.0) = 143.65N but this was incorrect.
EDIT: I've finally found the solution, so here's what I did.
First, calculate Work using the equation: (F-mgsin(theta))*displacement, where F=the force being applied by the push, theta is the angle of the ramp, and displacement is the length of the ramp.
Now that you have the value for work, set it equal to the work-energy theorem:
W = 1/2(mv_f^2)-1/2(mv_o^2). Plug in the values for work, mass and initial velocity, and solve for the final velocity, which is the answer to the question.
I've tried a few different ways but each was wrong. At first, I tried solving for acceleration and then using that to solve for final velocity but that was incorrect. I checked the hints given to me by Pearson which tell me to find the total work first, and looking at the hints for that, they said to find Fx,net which I thought I did correctly but apparently not. Attached is a simplified version of my thought process (including my free body diagram).
I know there's some relation between the force of gravity pointing down (being negative) so I also tried subtracting Fn-Fg and then adding the other forces and finding the component but that didn't work either. I also tried finding the x-component of each force and adding them together, but that didn't work.
Once I have that, I also need to find initial kinetic energy and total work to find the final speed, which I'm not confident in knowing how to do, but I'll cross that bridge when I get there.
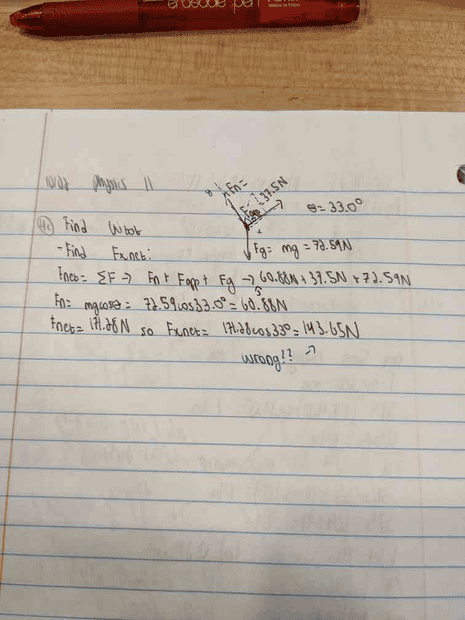
First, calculate Work using the equation: (F-mgsin(theta))*displacement, where F=the force being applied by the push, theta is the angle of the ramp, and displacement is the length of the ramp.
Now that you have the value for work, set it equal to the work-energy theorem:
W = 1/2(mv_f^2)-1/2(mv_o^2). Plug in the values for work, mass and initial velocity, and solve for the final velocity, which is the answer to the question.
I've tried a few different ways but each was wrong. At first, I tried solving for acceleration and then using that to solve for final velocity but that was incorrect. I checked the hints given to me by Pearson which tell me to find the total work first, and looking at the hints for that, they said to find Fx,net which I thought I did correctly but apparently not. Attached is a simplified version of my thought process (including my free body diagram).
I know there's some relation between the force of gravity pointing down (being negative) so I also tried subtracting Fn-Fg and then adding the other forces and finding the component but that didn't work either. I also tried finding the x-component of each force and adding them together, but that didn't work.
Once I have that, I also need to find initial kinetic energy and total work to find the final speed, which I'm not confident in knowing how to do, but I'll cross that bridge when I get there.
Last edited: