sams
Gold Member
- 84
- 2
In Chapter 11: Dynamics of Rigid Bodies, in the Classical Dynamics of Particles and Systems book by Thornton and Marion, Fifth Edition, pages 415-418, Section 11.3 - Inertia Tensor, I have three questions regarding the Inertia Tensor:
1.The authors made the following statement: "neither V nor ω is characteristic of the αth particle."
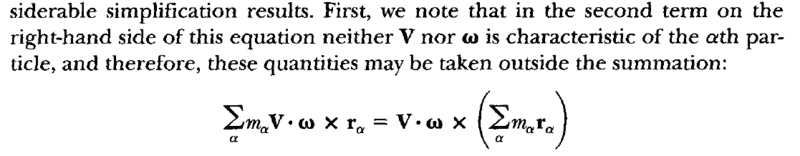
What do the authors mean by the above statement and how did they take V.ω outside the relation?
2. Kronecker delta function
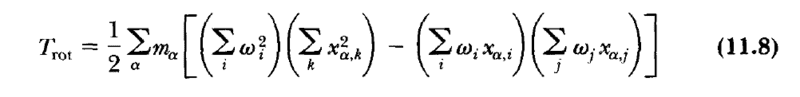
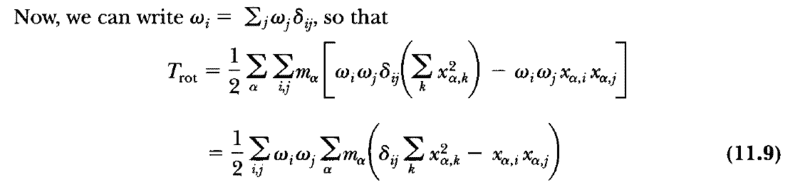
Shouldn't the second term in the square brackets or in the parenthesis of Equation (11.9) also contain the Kronecker delta function?
3. Physical Interpretation of the diagonals and off-diagonals of the Inertia Tensor
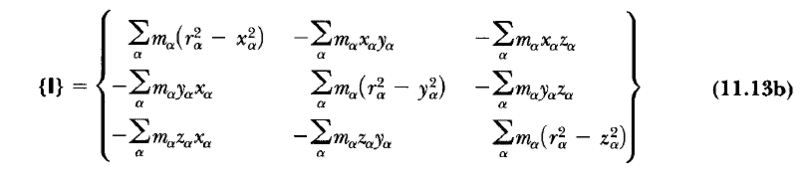
According to the authors, the diagonal terms are called the moments of inertia and the off-diagonal terms are called the products of inertia. What are the physical interpretations of the diagonal and the off-diagonal terms? What is the difference between them?
Thank you so much for your help.
1.The authors made the following statement: "neither V nor ω is characteristic of the αth particle."
What do the authors mean by the above statement and how did they take V.ω outside the relation?
2. Kronecker delta function
Shouldn't the second term in the square brackets or in the parenthesis of Equation (11.9) also contain the Kronecker delta function?
3. Physical Interpretation of the diagonals and off-diagonals of the Inertia Tensor
According to the authors, the diagonal terms are called the moments of inertia and the off-diagonal terms are called the products of inertia. What are the physical interpretations of the diagonal and the off-diagonal terms? What is the difference between them?
Thank you so much for your help.
Attachments
Last edited: