Quick question about the representation of error on a graph

[Ellio]

Homework Statement

Draw the graph x (t)

Relevant Equations

Y range = 0 to 0.621
X range = 0 to 0.135

Y tick distance = 0.0125
X tick distance = 0.00375

Hello I hope you are all very well. I did a graph for a physics practical work and I would like to put the "error bar" (I don't know if it's called like this, I'm sorry).
Something like this:

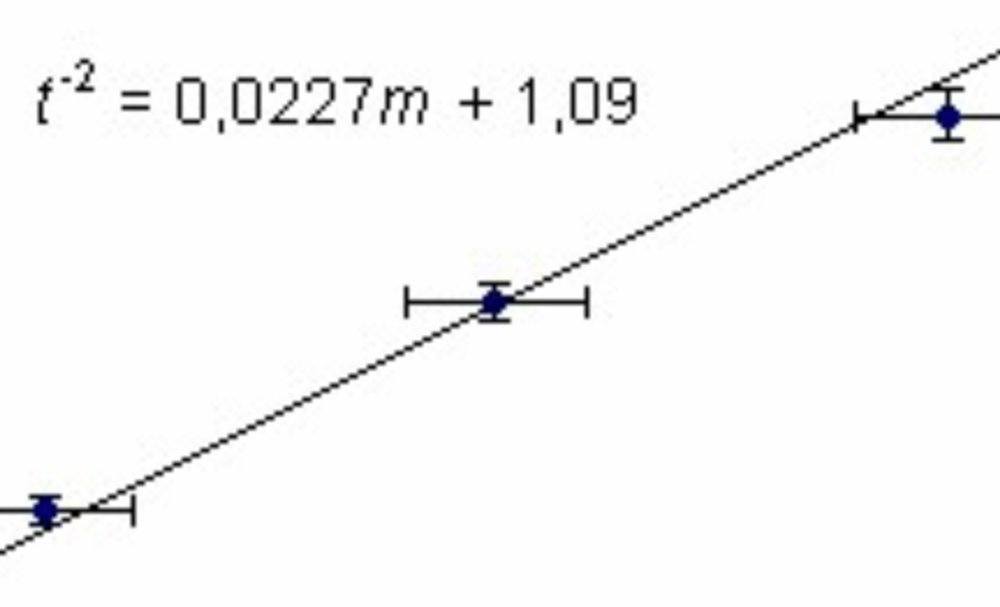
I just don't know how long the margin should be.

If someone could clarify to me the way to do the error bars, I would be really grateful.

 

[kuruman]

What you show is OK, but can you post the entire graph including the axes and their labels?

 

[Ellio]

What you show is OK, but can you post the entire graph including the axes and their labels?

Oh, the image I showed was just to clarify what I was talking about, it's not the graph I made.

This is the graph on which I would like to put the error bars.

 

[kuruman]

The plot is in illegible. I think you should use a canned program such as Excel to produce a plot. Excel will also put error bars for you so you will not have to draw them by hand. Are your error bars fixed in magnitude, a percentage of the values or what?

 

[Ellio]

The plot is in illegible. I think you should use a canned program such as Excel to produce a plot. Excel will also put error bars for you so you will not have to draw them by hand. Are your error bars fixed in magnitude, a percentage of the values or what?

There is no error bars yet. That's actually the topic of my question. I would like to know how to do error bars on a graphic (in percentage for example).

 

[kuruman]

Example
If x is 20 units and you have a 10% error then $x=20\pm 2~\mathrm{units}$. You put your point on the graph at x = 20 units and you draw two line segments, parallel to the x-axis, each 2 units long on either side of the point. Does that answer your question?

 

[Ellio]

Example
If x is 20 units and you have a 10% error then $x=20\pm 2~\mathrm{units}$. You put your point on the graph at x = 20 units and you draw two line segments, parallel to the x-axis, each 2 units long on either side of the point. Does that answer your question?

Ok but how do I determine the error percentage ?

 

[DEvens]

Ok but how do I determine the error percentage ?

Sorry, that's going to be in your data and the problem you are determining. "How do I determine the error percentage?" is not a question that could possibly be answered without going through your specific problem.

 

[Ellio]

Sorry, that's going to be in your data and the problem you are determining. "How do I determine the error percentage?" is not a question that could possibly be answered without going through your specific problem.

Oh ok so it isn't always 10% of one unit ? Could I in this case choose myself the percentage ?

 

[kuruman]

Ok but how do I determine the error percentage ?

You do not determine that, you estimate it. Only you know what you measured and how and it's not necessarily a percentage; it could be a fixed amount. For example, if you measured the length and width of a book using a standard ruler with millimeter subdivisions, you might say that you can measure the length to be $20 \pm 0.1~\mathrm{cm}$ which essentially means that you are pretty confident that the length of the book is not less than 19.9 cm or greater than 20.1 cm. The fact that the ruler has millimeter subdivisions does not necessarily mean that the error is fixed $\pm 0.1~\mathrm{cm}$. If you use the same ruler to measure the width of the book, you might have to report it as $12 \pm 0.3~\mathrm{cm}$ because the back of the book has some curvature in it and the "width" is not as well defined as the length. That's what I mean when I say "only you know what you measured and how". Do your best and use as your guide for setting the error bars the idea that there is not such a thing as the value of x but that x is limitied to a range of values beyond which it cannot have. The range of these values is the length of your error bar.

 

[Ellio]

You do not determine that, you estimate it. Only you know what you measured and how and it's not necessarily a percentage; it could be a fixed amount. For example, if you measured the length and width of a book using a standard ruler with millimeter subdivisions, you might say that you can measure the length to be $20 \pm 0.1~\mathrm{cm}$ which essentially means that you are pretty confident that the length of the book is not less than 19.9 cm or greater than 20.1 cm. The fact that the ruler has millimeter subdivisions does not necessarily mean that the error is fixed $\pm 0.1~\mathrm{cm}$. If you use the same ruler to measure the width of the book, you might have to report it as $12 \pm 0.3~\mathrm{cm}$ because the back of the book has some curvature in it and the "width" is not as well defined as the length. That's what I mean when I say "only you know what you measured and how". Do your best and use as your guide for setting the error bars the idea that there is not such a thing as the value of x but that x is limitied to a range of values beyond which it cannot have. The range of these values is the length of your error bar.

Understood, thank you so much for your help I appreciate it !