- #1
Cheesycheese213
- 55
- 8
- Homework Statement
- Calculate the uncertainty of a value (n) calculated by the equation n=1.0003tanθ
- Relevant Equations
- (shown below)
For a lab, I needed to calculate the uncertainty of a refractive index that was found using Snell's law. I found an equation online for propagation of error for any general function, which was
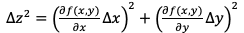
I thought that since my equation was
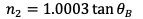
I could just get rid of the variable y, and have
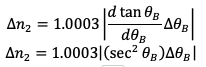
After inputting my values θ = 53.61 and Δθ = 0.1, I got
Δn = 0.284193...
Which I was sort of confused by? My value for n itself is only around 1.357, and I wasn't sure why the uncertainty was so large in comparison. I was wondering if I did something wrong?
For more context, I am calculating n for many different angles, and when graphing the values either the error bars look really big, or the slope is almost insignificant from the scale.
Thanks!
I thought that since my equation was
I could just get rid of the variable y, and have
After inputting my values θ = 53.61 and Δθ = 0.1, I got
Δn = 0.284193...
Which I was sort of confused by? My value for n itself is only around 1.357, and I wasn't sure why the uncertainty was so large in comparison. I was wondering if I did something wrong?
For more context, I am calculating n for many different angles, and when graphing the values either the error bars look really big, or the slope is almost insignificant from the scale.
Thanks!