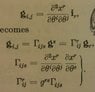osnarf
- 207
- 0
Hey everyone,
This formula was just provided in a book and I was trying to prove it but I'm having a hard time understanding what it's saying. The formula is attached, along with the definitions given for the Christoffel symbols. In the definitions the i's are the standard basis vectors and the x's are the coordinates associated with them.
I've been playing with it for a while and can't figure out what each symbol is supposed to mean in the context of the formula.
Just to make it easier to type, in this context does a symbol of the first kind [i j, k] with a bar over it mean
\frac{\partial^{2}\vartheta^{m}}{\partial\overline{\vartheta}^{i}\partial\overline{\vartheta}^{j}}*\frac{\partial\vartheta^{m}}{\partial\overline{\vartheta}^{k}},
or does it mean the same but with the thetas on top replaced with the standard basis coordinates?
The same question goes for the first order symbol with no bar, would this be the same as defined in the picture (w/r/t the standard basis), or is it the same as the Tex above but with the bars moved from the thetas on bottom to the thetas on top?
Thanks, your help is very appreciated.
edit - no idea why that one theta won't show up, sorry
This formula was just provided in a book and I was trying to prove it but I'm having a hard time understanding what it's saying. The formula is attached, along with the definitions given for the Christoffel symbols. In the definitions the i's are the standard basis vectors and the x's are the coordinates associated with them.
I've been playing with it for a while and can't figure out what each symbol is supposed to mean in the context of the formula.
Just to make it easier to type, in this context does a symbol of the first kind [i j, k] with a bar over it mean
\frac{\partial^{2}\vartheta^{m}}{\partial\overline{\vartheta}^{i}\partial\overline{\vartheta}^{j}}*\frac{\partial\vartheta^{m}}{\partial\overline{\vartheta}^{k}},
or does it mean the same but with the thetas on top replaced with the standard basis coordinates?
The same question goes for the first order symbol with no bar, would this be the same as defined in the picture (w/r/t the standard basis), or is it the same as the Tex above but with the bars moved from the thetas on bottom to the thetas on top?
Thanks, your help is very appreciated.
edit - no idea why that one theta won't show up, sorry
Attachments
Last edited: