pcandrepair
- 65
- 0
Rate of revolution for a dryer?!?
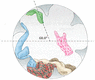
In a home laundry dryer, a cylindrical tub containing wet clothes is rotated steadily about a horizontal axis as shown in the figure below. So that the clothes will dry uniformly, they are made to tumble. The rate of rotation of the smooth-walled tub is chosen so that a small piece of cloth will lose contact with the tub when the cloth is at an angle of 62.5° above the horizontal. If the radius of the tub is 0.385 m, what rate of revolution is needed? (revs/min)
2. The attempt at a solution
First I found the velocity of the dryer tub:
Cos(62.5) = (v^2)/gR
Cos(62.5) = (v^2)/9.8(.385)
v = 1.32m/s
Then I used that velocity to find the rate of revolution:
(v/2(pi)(.385)) * 60sec = 32.74 Revolutions/min
I submitted this answer and it said it was wrong. I can't seem to see what I did wrong. Any help or suggestions would be appreciated. Thanks.
Homework Statement
In a home laundry dryer, a cylindrical tub containing wet clothes is rotated steadily about a horizontal axis as shown in the figure below. So that the clothes will dry uniformly, they are made to tumble. The rate of rotation of the smooth-walled tub is chosen so that a small piece of cloth will lose contact with the tub when the cloth is at an angle of 62.5° above the horizontal. If the radius of the tub is 0.385 m, what rate of revolution is needed? (revs/min)
2. The attempt at a solution
First I found the velocity of the dryer tub:
Cos(62.5) = (v^2)/gR
Cos(62.5) = (v^2)/9.8(.385)
v = 1.32m/s
Then I used that velocity to find the rate of revolution:
(v/2(pi)(.385)) * 60sec = 32.74 Revolutions/min
I submitted this answer and it said it was wrong. I can't seem to see what I did wrong. Any help or suggestions would be appreciated. Thanks.