DeadFlower
- 3
- 0
Hi!
V = IR
Kirchhoff Current and Voltage Law.
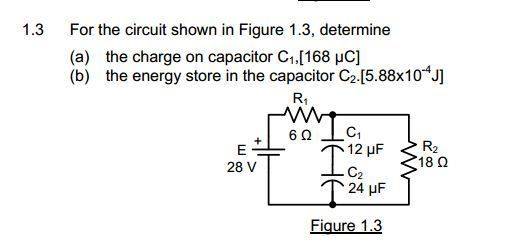
I am facing difficulty with this RC circuit.
I tried looking up solutions but all I could find were either exclusively series or parallel.
My first guess was to take Total Current = 28/(6+18). However, that ended up being wrong.
I worked backwards from the answer provided and realized that Current through R2 = 28/(6+18) instead of what I thought earlier. However, I am unable to relate this to any of the formula I can find.I would be a great help if someone were able to explain to me how to arrive and the solutions to the question.
Thanks.
Homework Statement
Homework Equations
V = IR
Kirchhoff Current and Voltage Law.
The Attempt at a Solution
I am facing difficulty with this RC circuit.
I tried looking up solutions but all I could find were either exclusively series or parallel.
My first guess was to take Total Current = 28/(6+18). However, that ended up being wrong.
I worked backwards from the answer provided and realized that Current through R2 = 28/(6+18) instead of what I thought earlier. However, I am unable to relate this to any of the formula I can find.I would be a great help if someone were able to explain to me how to arrive and the solutions to the question.
Thanks.
Attachments
Last edited: