SUMMARY
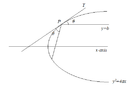
The discussion focuses on the reflection of a ray of light from a concave mirror defined by the parabola equation \(y^2 = 4ax\). The point of incidence is established as \(\left(\frac{b^2}{4a}, b\right)\). Using the law of reflection, the slope of the reflected ray is derived as \(m = \frac{4ab}{b^2 - 4a^2}\), leading to the equation of the reflected ray \(y - b = \frac{4ab}{b^2 - 4a^2}\left(x - \frac{b^2}{4a}\right)\). It is conclusively shown that this reflected ray passes through the focus of the parabola at \((a, 0)\).
PREREQUISITES
- Understanding of parabolic equations, specifically \(y^2 = 4ax\)
- Knowledge of the law of reflection in optics
- Familiarity with calculus concepts such as derivatives and slopes
- Ability to manipulate trigonometric identities and equations
NEXT STEPS
- Study the properties of parabolas and their applications in optics
- Learn about the derivation and applications of the law of reflection
- Explore tangent lines to curves and their significance in calculus
- Investigate the geometric interpretations of slopes and angles in reflection scenarios
USEFUL FOR
Students and professionals in physics, particularly those studying optics, as well as mathematicians interested in the properties of parabolas and their applications in real-world scenarios.