Any equation that fits in this shape? (variable concavity)

[mikejm]

I'm working on an audio synthesis project and I need an equation that can create these lines:

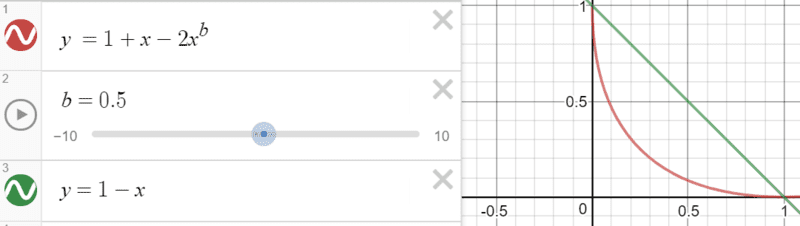
That is, I would like an equation that describes a line that always passes through (0,1) and (1,0), and has a single coefficient parameter that can be varied to create functions of intermediate concavity/convexity like the red line shown.

The concavity/convexity should be symmetric as if mirrored along the line of y=x between the boundaries of (0,1) and (1,0). Anything outside that range is irrelevant.

Is there an equation that can do this?

 

[.Scott]

If I set the center of circle to be (x,y) = (b,b) for b>=1, and then set the radius of the circle to cross through (1,0) and (0,1):
r = sqrt(bb+ (bb-1)) = sqrt(2bb - 1)
then the equation for the circle will be:
(x-b)^2 + (y-b)^2 = bb +(b-1)^2
xx-2xb+bb+yy-2yb+bb = 2bb-2b+1
xx-2xb+bb+yy-2yb+bb-2bb+2b-1 = 0
xx-2xb+yy-2yb+2b-1 = 0
y = (2b+/-sqrt(2bb-4(xx-2xb+2b-1)))/2
y = b+/-sqrt(bb-(xx-2xb+2b-1))

but we only want the bottom of the circle, so:
y = b-sqrt(bb-(xx-2xb+2b-1))

 

[mfb]

$(1-x)^a + (1-y)^a = 1$ - this can be solved for y if you prefer that: $y=1-(1-(1-x)^a)^{1/a}$

a=1 gives a straight line, a=2 gives a quarter-circle, larger a give something that passes closer to (0,0). It is always symmetric as you can see from the first equation.
Example curves.