Relating flow rate to height in a cylinder

[TsuinRyu]

Hi, so I am trying to calculate the maximum height that would be achieved in a cylinder and have been give only the flow rate.

View attachment Flow data.xls

The cylinder itself is a simple straight sided cylinder, the opening at the top has a diameter of 5cm and the hole at the bottom has a diameter of 0.5cm

http://imageshack.us/photo/my-images/407/pic1ub8.jpg/

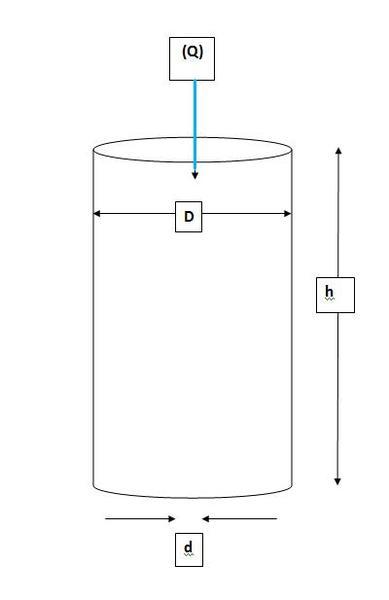
I believe that I need to calculate the rate at which the liquid escapes from the small hole, and the point at which flow in = flow out will result in maximum height. But I am unable to work out how to apply this to the data I have? I also am not sure how to apply Bernoulli's equation to this.

Any help is appreciated

Thank you

 

[Simon Bridge]

Use your understanding of physics...
What determines the rate that material goes through the small hole?

 

[TsuinRyu]

Unfortunately I am a medic and have done no physics in the last 6 years. But I assume the flow out is dependant upon gravity acting upon the body of fluid in the cylinder?

I've seen the equation v^2=2gh (where h is change in height) but I can't work out how to solve it as the flow rate I have is into the cylinder, plus I need to work out the height.

 

[Simon Bridge]

Presumably you have some course notes - you are not expected to do this blind?

You will have either a volume or a mass flow rate.
You can get the volume flow rate from the mass rate using the mass density.
The volume flow rate is the rate the volume is changing.

What is the equation for the volume of a cylinder with height h and diameter D?
How does h change when the volume changes?

If v is the speed that liquid leaves through a hole with cross-section area A, then what volume of liquid leaves through the hole per second?

 

[TsuinRyu]

I have no course notes, hence the difficulty in solving this.

The data we have is the flow rate into the cylinder and I have the diameter of the cylinder D=5cm and the diameter of the hole at the bottom of the cylinder d=0.5cm

As I understand it you have to make the assumption that pressure at any point is 0 as the cylinder is open at both end. I believe to solve this you also have to assume that density is the same through out and that the fluid experiences no friction.

I understand that the flow rate is the change in volume per second, but how can I use this to work out height?

Equation for the volume of a cylinder V=πr²h

As Volume increases so will the height, but I do not have the volume, but the flow rate? And how would I account for the loss of fluid through the smaller hole at the bottom? (from what I understand v²=2gΔh where v is the flow out of the small hole. I have seen another equation where Q=A√2gΔh, is this the one I should be using for flow out of the small hole?)

Thank you

 

[Simon Bridge]

I have no course notes, hence the difficulty in solving this.

Yo are doing a course that has no course notes?
What do they just give you problems to solve and no idea what you are expected to be learning?
Does the course have a title at least?

Anyway - I think I have a handle on what you need.

Notes:
You seem to be hunting almost blindly for the "right equation".
You should not do this - instead think about what is going on in the physics of the problem.
Then you have to construct your own equation which describes that. There will be a lot of steps and you won't always know all the bits each step of the way.

eg.
The liquid drops a distance h from the top of the tank before it can go through the hole. This means it loses gravitational potential energy, which turns into kinetic energy through the hole. So you can write:

$mgh=\frac{1}{2}mv^2 \Rightarrow v^2=2gh$ ... which tells you how fast the liquid leaves the tank. You need to turn this into a volume that it leaves the tank. Don't worry about not knowing the height, that's what you are doing all this math to find out. You will end up with an equation that goes $h=\cdots$ some other stuff that you do know.

What you know, is (1) a relationship between height and speed-out, and (2) the rate liquid gets in.
You need to find out the maximum height: when the tank is at max-height, $v^2=2gh_{max}$ ... progress!

The max-height would be when the volume is a maximum ... and you have an equation which relates volume to height $V=\pi r^2 h$

... so you only need to find the maximum volume and put it into that equation to find the maximum height.

When the volume is a maximum, there will be a special relationship between the rate coming in and the rate leaving. What is it?

You are given the rate coming in $Q_{in}$ ... you still need the rate going out $Q_{out}$. You have an equation for the speed that the liquid is leaving and the area of the hole.

Consider:
If liquid leaves a tank at speed v m/s, through a hole of area A m², then what volume of liquid leaves the tank in one second?

 

[TsuinRyu]

The course is called Bio-engineering in Urology and this is supposed to be urine flow rate data.

Right so at h_max I believe that Q_in = Q_out

Q_out=vA, where v=$\sqrt{2gh}$ and A=$\pi$r²

therefore Q_out=$\pi$r²$\sqrt{2gh}$

I also know that Q=$\frac{dV}{dt}$...using this for Q_in:

$\frac{dV}{dt}$=$\pi$r²$\sqrt{2gh}$?

Where V=$\pi$r²h

this is the point I become very confused as I get get h_max=2g.t²( $\frac{R2}{R1}$ )⁴

But this suggests that as time increases the h_max will continue to increase. However as the the data in the spreadsheet shows the flow rate in stops, but the flow rate out will continue till there is no fluid in the cylinder, hence height should start to decrease when Q_out>Q_in? So clearly I've done something wrong here?


Or is it:

h_max=v²/2g (1)

V_max=$\pi$r²h_max (2)

∴ V_max=$\pi$r₁². v²/2g

As v=$\frac{Q}{A}$ (3)


∴ V_max=$\pi$r₁². (Q/A)²/2g...where A is the area of the exit hole ($\pi$r₂²), but then I don't really have the flow rate for the exit

I seem unable to bring in the flow rate data I have into these equations other than when the flow rate out equals the flow rate in the height will be maximum.

 

[Simon Bridge]

Close: $\frac{dV}{dt}$ is the rate that the volume changes over time - which is the difference between the rate you pour stuff in and the rate that stuff leaves - make sense?
$\frac{dV}{dt}=Q_{in}-Q_{out}$

You now need to look at the flow rate data and think about what "flow rate" actually means. What is it that is being measured in that data?

 

[TsuinRyu]

So the flow rate data is the rate of change of volume per second. It is measuring the amount of fluid entering the cylinder per second?

Sorry I'm just really confused

 

[Simon Bridge]

The change of volume over time is written $\frac{dV}{dt}$ ... this will be the difference between the volume-rate you put in and the volume-rate you take out. Hence: $\frac{dV}{dt}=Q_{in}-Q_{out}$. Since $Q_{out}$ depends on the height, the max height is reached when $\frac{dV}{dt}=0$.

However, you have a lot of data over time in your sheets.
It seems to relate to volumes and times but volumes of what?
There are lots of ways to measure flow... eg. is this the volume of urine in the bottle at different time intervals? The difference in volume at different time intervals, divided by the time interval? The rate recorded by some meter on the inflow valve? What?

I want you to concentrate on telling me how this data was collected.

If you just had a constant $Q_{in}$ given to you then the problem would be easy. However, the patient is not cooperating by producing a continuous stream of urine all the time.