Homework Help Overview
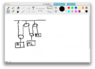
The discussion revolves around understanding the relationship of acceleration between three masses, m1, m2, and m3, in a pulley system where m1 is greater than m2, which is greater than m3. The setup involves both free and fixed pulleys, with specific constraints on the motion of the masses.
Discussion Character
Approaches and Questions Raised
- Participants explore different equations relating the accelerations of the masses, with some suggesting the use of Lagrangian mechanics versus Newton's second law. There are questions about the setup, particularly regarding the movement of the masses and the implications of their respective accelerations.
Discussion Status
Participants are actively engaging with the problem, sharing equations and discussing the implications of their assumptions. Some guidance has been offered regarding the relationship between the accelerations, but there is no explicit consensus on the correct approach or solution yet.
Contextual Notes
There are constraints regarding the assumptions that can be made about the motion of the masses, as well as the need for clarity in the setup, which is complicated by the presence of multiple pulleys. The specific masses of m1, m2, and m3 have been provided, but their influence on the acceleration relationship is still under discussion.