knowLittle
- 307
- 3
Homework Statement
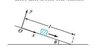
At time t=0, a block is released from point O on the slope shown in the figure.
The block accelerates down the slope, overcoming sliding friction.
a.) Choose axes 0xy as shown, and solve the equation ##\Sigma F = m a## into its x and y components.
Hence find the block's position (x,y) as a function of time, and the time it takes to reach the bottom.
b.) Carry out the solution using the axes Ox'y', with Ox' horizontal and Oy' vertical, and show that you get the same final answer. Explain why the solution using these axes is less convenient.
Homework Equations
distance =v*t
The Attempt at a Solution
Normal force = mg
## m*g* cos(\theta) = ##force perpendicular to the base not the ramp
y=0 in the 0xy frame.
I know that to obtain x I need to subtract the friction force upwards.
However, I am having problems finding x.
So, Fnet_x = Fx - F_friction
Fx= hypotenuse*cos##(\theta)##
Help.