Replace a Toffoli gate with an equivalent circuit

[Peter_Newman]

Hello,

I am currently working on this task here. Given is a Toffoli gate. Now it is stated that there is an equivalent quantum circuit. I tried to show the equivalence, for example by looking at case $|111\rangle$.

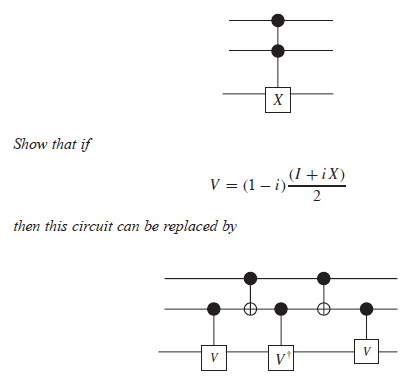
However, with what I have calculated so far, I do not come to the conclusion that the circuits are equivalent.
I have rewritten the term V first:

$$V=(1-i)\frac{I+iX}{2}=\begin{pmatrix}0.5-0.5i&0.5+0.5i\\0.5+0.5i&0.5-0.5i\end{pmatrix}$$
Now I just start with the case $|111\rangle$. This should, because it comes to the equivalence dof the Toffoli gate at the end of $|110\rangle$ come out.

$$|111\rangle\xrightarrow{V} |11\rangle\begin{pmatrix}0.5-0.5i&0.5+0.5i\\0.5+0.5i&0.5-0.5i\end{pmatrix}\begin{pmatrix}0\\1\end{pmatrix}=|11\rangle\begin{pmatrix}0.5+0.5i\\0.5-0.5i\end{pmatrix}\xrightarrow{CNOT}|10\rangle\begin{pmatrix}0.5+0.5i\\0.5-0.5i\end{pmatrix}$$

$$\left(V^T\right)^{*}=\begin{pmatrix}0.5+0.5i&0.5-0.5i\\0.5-0.5i&0.5+0.5i\end{pmatrix}$$

$$|10\rangle\begin{pmatrix}0.5+0.5i\\0.5-0.5i\end{pmatrix}\xrightarrow{\left(V^T\right)^{*}} |10\rangle\begin{pmatrix}0.5+0.5i&0.5-0.5i\\0.5-0.5i&0.5+0.5i\end{pmatrix}\begin{pmatrix}0.5+0.5i\\0.5-0.5i\end{pmatrix}=|10\rangle|1\rangle$$

$$|10\rangle|1\rangle\xrightarrow{CNOT} |11\rangle|1\rangle\xrightarrow{V}|11\rangle\begin{pmatrix}0.5-0.5i&0.5+0.5i\\0.5+0.5i&0.5-0.5i\end{pmatrix}\begin{pmatrix}0\\1\end{pmatrix}=|11\rangle\begin{pmatrix}0.5+0.5i\\0.5-0.5i\end{pmatrix}\neq |110\rangle$$

It could be that I made a mistake in my calculation. What do you all mean?

 

[tnich]

$$|10\rangle\begin{pmatrix}0.5+0.5i\\0.5-0.5i\end{pmatrix}\xrightarrow{\left(V^T\right)^{*}} |10\rangle\begin{pmatrix}0.5+0.5i&0.5-0.5i\\0.5-0.5i&0.5+0.5i\end{pmatrix}\begin{pmatrix}0.5+0.5i\\0.5-0.5i\end{pmatrix}=|10\rangle|1\rangle$$

In this step since the second qubit has a value of $\left |0\right>$, the $V^*$ gate should not be applied according to your circuit diagram.

 

[tnich]

In this step since the second qubit has a value of $\left |0\right>$, the $V^*$ gate should not be applied according to your circuit diagram .

By the way, it seems much easier to keep the bra-ket notation in this case rather than revert to matrices. For example, the first step becomes
$$|111\rangle\xrightarrow{V} |11\rangle\frac 1 2 (1-i)(I+iX)\left|1\right> = \frac 1 2 (1-i)|11\rangle(\left|1\right>+i\left|0\right>)$$
Also, I think there is an error in the problem statement. In paper that described this method, Elementary gates for quantum computation (PhysRevA.52.3457), the equivalent Toffoli gate is given as

where in this case $U=V^2=X$. Note that the last controlled(V) gate is controlled by a different bit than the first one.